题目内容
已知实数a≠0,函数f(x)=ax(x-2)2(x∈R)有极大值32,则实数a等于______.
27
本题考查函数的极值.可导函数极值点处的导数为0.
f(x)=ax(x2-4x+4)=ax3-4ax2+4ax,
∴f′(x)=3ax2-8ax+4a=a(3x2-8x+4)=a(3x-2)(x-2).
令f′(x)=0,得x1=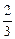 或x2=2.
或x2=2.
∴在x1=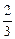 或x2=2处取得极值.把x=2代入验证,极值为0,
或x2=2处取得极值.把x=2代入验证,极值为0,
因此函数在x=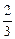 处取得极值32,即a×
处取得极值32,即a×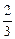 ×(
×(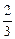 -2)2=32.
-2)2=32.
解得a=27.
f(x)=ax(x2-4x+4)=ax3-4ax2+4ax,
∴f′(x)=3ax2-8ax+4a=a(3x2-8x+4)=a(3x-2)(x-2).
令f′(x)=0,得x1=
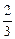 或x2=2.
或x2=2.∴在x1=
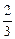 或x2=2处取得极值.把x=2代入验证,极值为0,
或x2=2处取得极值.把x=2代入验证,极值为0,因此函数在x=
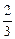 处取得极值32,即a×
处取得极值32,即a×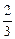 ×(
×(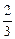 -2)2=32.
-2)2=32.解得a=27.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
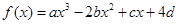 (
(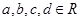 )的图象关于原点对称,且
)的图象关于原点对称,且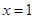 时,
时,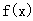 取极小值
取极小值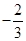 ,
,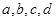 的值;
的值; 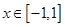 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。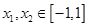 ,求证:
,求证: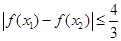 。
。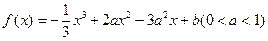
 ,求a的取值范围.
,求a的取值范围.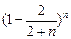
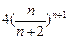
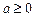 ,
,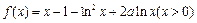 .令
.令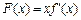 ,讨论
,讨论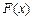 在
在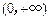 内的单调性并求极值;
内的单调性并求极值;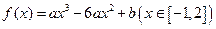 的最大值为
的最大值为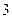 ,最小值为
,最小值为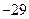 ,求
,求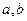 。
。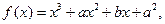 在
在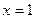 时有极值
时有极值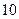 ,那么
,那么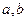 的值分别为_
的值分别为_