题目内容

15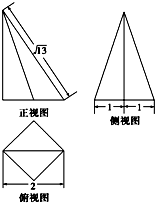．某空间几何体的底面为正方形，其三视图如图所示，则该空间几何体的体积等于（　　）
A．1B．2C．3D．4

分析 由已知中的三视图，可知该几何体是一个以俯视图为底面的锥体，分别计算底面面积和高，代入锥体体积公式，可得答案．

解答 解：由已知中的三视图，可知该几何体是一个以俯视图为底面的锥体，
锥体的底面面积S=$\frac{1}{2}$×2×2=2，
锥体的高h=$\sqrt{{\sqrt{13}}^{2}-{2}^{2}}$=3，
故锥体的体积V=$\frac{1}{3}Sh$=2，
故选：B

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案
相关题目
5．设a∈R，函数f（x）=2x2+（x-a）|x-a|，g（x）=lnx；
（1）若f（0）=1，试判断y=f[g（x）]在[e，+∞）上的单调性（无需证明）；
（2）求f（x）的最小值；
（3）设h（x）=2x2+（3a-2）x-（5a2-7a-3），且x∈（a，+∞），求不等式f（x）＞h（x）的解集．
6．已知全集U={1，2，3，4，5}，集合 A={1，4}，B={1，3，5}，则（∁UA）∩（∁UB）=（　　）
A．{2}B．{1，2}C．{3，5}D．{4，5}
3．“a=1”是“直线y=x与函数y=ln（x+a）的图象有且仅有一个交点”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
10．已知点A（$\frac{π}{8}$，f（$\frac{π}{8}$））和直线x=$\frac{3π}{8}$分别是函数f（x）=2$\sqrt{2}$sin?xsin（?x+$\frac{π}{4}$）（?＞0）相邻的一个对称中心和一条对称轴，将函数f（x）的图象向右平移φ个单位得到函数g（x）的图象，若当x=$\frac{π}{3}$时，g（x）取最大值，则g（x）在[-$\frac{π}{2}$，0]上单调增区间为[-$\frac{π}{6}$，0]．
20．已知函数f（x）=2cos2$\frac{x}{2}$+$\sqrt{3}$sinx．
（1）求函数f（x）的最小正周期和值域；
（2）若α为第二象限角，且f（α+$\frac{π}{3}$）=-$\frac{1}{5}$，求$\frac{cos2α}{1-tanα}$的值．
7．已知y=f（x）（x∈D，D为此函数的定义域）同时满足下列两个条件：①函数f（x）在D内单调递增或单调递减；②如果存在区间[a，b]⊆D，使函数f（x）在区间[a，b]上的值域为[a，b]，那么称y=f（x），x∈D为闭函数；
请解答以下问题
（1）求闭函数y=-x3符合条件②的区间[a，b]；
（2）判断函数f（x）=x+$\frac{1}{x}$（x∈（0，+∞））是否为闭函数？并说明理由；
（3）若y=k+$\sqrt{x}$是闭函数，求实数k的取值范围．
4．若复数Z满足（2-i）2Z=1（i为虚数单位）．则复数Z的虚部为$\frac{4}{25}$．
5．设函数fn（x）=n2x2（1-x）n（n为正整数），则fn（x）在[0，1]上的最大值为（　　）
A．0B．1C．（1-$\frac{2}{2+n}$）nD．4（$\frac{2}{2+n}$）n+2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网