题目内容
3.“a=1”是“直线y=x与函数y=ln(x+a)的图象有且仅有一个交点”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 求函数的导数,利用导数的几何意义求出对应的切线方程,根据充分条件和必要条件的定义进行判断即可.
解答 解:若直线y=x与函数y=ln(x+a)的图象有且仅有一个交点,
则直线y=x与函数y=ln(x+a)的图象相切,
函数y=ln(x+a)的导数为f′(x)=$\frac{1}{x+a}$,
设切点坐标为(m,n),则切线斜率k=f′(m)=$\frac{1}{m+a}$,f(m)=ln(m+a)
则切线方程为y-ln(m+a)=$\frac{1}{m+a}$(x-m),
即y=$\frac{1}{m+a}$•x+ln(m+a)-$\frac{m}{m+a}$,
即$\frac{1}{m+a}$=1,ln(m+a)-$\frac{m}{m+a}$=0,
即m+a=1,m=0,则a=1,
当a=1时,直线y=x与函数y=ln(x+1)相切只有一个交点,
故“a=1”是“直线y=x与函数y=ln(x+a)的图象有且仅有一个交点”的充分条件和必要条件,
故选:C.
点评 本题主要考查充分条件和必要条件以及导数的几何意义,将问题转化为求函数的切线方程是解决本题的关键.

练习册系列答案
相关题目
14.某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取M名同学的成绩,数据的分组统计表如下:
(1)求出表中M,n的值;
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在(40,60]中的6位同学中任意抽取2人进行调查,求分数在(40,50]和(50,60]中各有一人的概率.
| 分组 | 频数 | 频率 | 频率/组距 |
| (40,50] | 2 | 0.02 | 0.002 |
| (50,60] | 4 | 0.04 | 0.004 |
| (60,70] | 11 | 0.11 | 0.011 |
| (70,80] | 38 | 0.38 | 0.038 |
| (80,90] | m | n | p |
| (90,100] | 11 | 0.11 | 0.011 |
| 合计 | M | N | P |
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在(40,60]中的6位同学中任意抽取2人进行调查,求分数在(40,50]和(50,60]中各有一人的概率.
11.若曲线y=ex-$\frac{a}{e^x}$(a>0)上任意一点切线的倾斜角的取值范围是[${\frac{π}{3}$,$\frac{π}{2}}$),则a=( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | 3 |
18.为了考查培育的某种植物的生长情况,从试验田中随机抽取50株该植物进行检测,得到该植物高度的频数分布表如下:
(Ⅰ)写出表中①②③④处的数据;
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第4组的概率.
| 组序 | 高度区间 | 频数 | 频率 |
| 1 | [230,235) | 8 | 0.16 |
| 2 | [235,240) | ① | 0.24 |
| 3 | [240,245) | ② | 0.20 |
| 4 | [245,250) | 10 | ③ |
| 5 | [250,255] | 5 | ④ |
| 合计 | 50 | 1.00 | |
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第4组的概率.
15.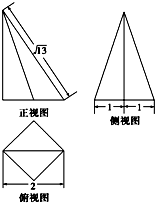 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面 ADD1A1.
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面 ADD1A1.