题目内容
20.已知函数f(x)=2cos2$\frac{x}{2}$+$\sqrt{3}$sinx.(1)求函数f(x)的最小正周期和值域;
(2)若α为第二象限角,且f(α+$\frac{π}{3}$)=-$\frac{1}{5}$,求$\frac{cos2α}{1-tanα}$的值.
分析 (1)由条件利用二倍角公式化简函数的解析式,再根据正弦函数的周期性和值域求得f(x)的最小正周期和值域.
(2)由条件利用同角三角函数的基本关系,二倍角公式,以及三角函数在各个象限中的符号求得cosα 的值,可得 sinα和 tanα
的值,从而求得$\frac{cos2α}{1-tanα}$的值.
解答 解:(1)由于函数f(x)=2cos2$\frac{x}{2}$+$\sqrt{3}$sinx=cosx+$\sqrt{3}$sinx+1=2sin(x+$\frac{π}{6}$)+1,
故函数f(x)的最小正周期为$\frac{2π}{1}$=2π,再根据sin(x+$\frac{π}{6}$)∈[-1,1],可得函数f(x)的值域为[-1,3].
(2)∵α为第二象限角,且f(α+$\frac{π}{3}$)=2sin(α+$\frac{π}{2}$)+1=2cosα+1=-$\frac{1}{5}$,
∴cosα=-$\frac{3}{5}$,∴sinα=$\frac{4}{5}$,tanα=-$\frac{4}{3}$,
∴$\frac{cos2α}{1-tanα}$=$\frac{{2cos}^{2}α-1}{1-tanα}$=$\frac{2×\frac{9}{25}-1}{1+\frac{4}{3}}$=-$\frac{3}{25}$.
点评 本题主要考查同角三角函数的基本关系,二倍角公式,以及三角函数在各个象限中的符号,正弦函数的周期性和值域,属于基础题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
10.已知ABCD-A1B1C1D1是边长为1的正方体,P为线段AB1上的动点,Q为底面ABCD上的动点,则PC1+PQ最小值为( )
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{{1+\sqrt{5}}}{2}$ |
11.若曲线y=ex-$\frac{a}{e^x}$(a>0)上任意一点切线的倾斜角的取值范围是[${\frac{π}{3}$,$\frac{π}{2}}$),则a=( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | 3 |
15.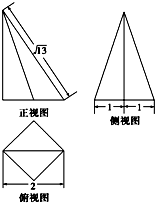 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.函数y=lg(-x2+2x+8)的增区间为( )
| A. | (-∞,1] | B. | [1,+∞) | C. | (-2,1] | D. | [1,4) |
 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面 ADD1A1.
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面 ADD1A1.