题目内容
7.已知y=f(x)(x∈D,D为此函数的定义域)同时满足下列两个条件:①函数f(x)在D内单调递增或单调递减;②如果存在区间[a,b]⊆D,使函数f(x)在区间[a,b]上的值域为[a,b],那么称y=f(x),x∈D为闭函数;请解答以下问题
(1)求闭函数y=-x3符合条件②的区间[a,b];
(2)判断函数f(x)=x+$\frac{1}{x}$(x∈(0,+∞))是否为闭函数?并说明理由;
(3)若y=k+$\sqrt{x}$是闭函数,求实数k的取值范围.
分析 (1)根据“闭函数”的定义,结合y=-x3的单调性,列出方程组,求出a、b的值;
(2)根据f(x)在区间(0,+∞)上不是单调函数,得出f(x)在(0,+∞)上不是“闭函数”;
(3)先判断g(x)=k+$\sqrt{x}$在定义域[0,+∞)上的单调性,再根据“闭函数”的定义列出方程组,利用转化思想求出k的取值范围.
解答 解:(1)因为y=-x3在R上是减函数,若在区间[a,b]上是“闭函数”,
则$\left\{\begin{array}{l}-{a^3}=b\\-{b^3}=a\end{array}\right.$,且a<b,
解得$\left\{\begin{array}{l}a=-1\\ b=1\end{array}\right.$;
所以满足条件的区间为[-1,1];
(2)由f(x)=x+$\frac{1}{x}$(x∈(0,+∞)得
$f(\frac{1}{2})=\frac{5}{2},f(1)=2,f(2)=\frac{5}{2}$,
所以f(x)在(0,+∞)上不是单调函数,不符合“闭函数”定义,
所以f(x)=x+$\frac{1}{x}$在x∈(0,+∞)上不是“闭函数”;
(3)设g(x)=k+$\sqrt{x}$,则g(x)的定义域为[0,+∞),
在[0,+∞)内任取x1<x2,
则$g({x_1})-g({x_2})=\sqrt{x_1}-\sqrt{x_2}$=$\frac{{{x_1}-{x_2}}}{{\sqrt{x_1}+\sqrt{x_2}}}$<0;
所以g(x1)<g(x2),
所以g(x)是增函数.
设符合条件的区间为[a,b],则有g(a)=a,g(b)=b,
即$\left\{\begin{array}{l}k+\sqrt{a}=a\\ k+\sqrt{b}=b\end{array}\right.$,
所以a、b是方程x-$\sqrt{x}$-k=0的两根;
所以问题转化为h(x)=x2-x-k有两个非负零点,
即方程x2-x-k=0在[0,+∞)内有两个不同实数根;
所以$\left\{\begin{array}{l}△={(-1)^2}-4(-k)>0\\{x_1}+{x_2}=1>0\\{x_1}{x_2}=-k≥0\end{array}\right.$,
解得-$\frac{1}{4}$<k≤0,
所以,实数k的取值范围是$(-\frac{1}{4},0]$.
点评 本题考查了新定义的问题,考查了函数的性质与应用问题,考查了方程思想与转化思想的应用问题,是综合性题目.

| 组序 | 高度区间 | 频数 | 频率 |
| 1 | [230,235) | 8 | 0.16 |
| 2 | [235,240) | ① | 0.24 |
| 3 | [240,245) | ② | 0.20 |
| 4 | [245,250) | 10 | ③ |
| 5 | [250,255] | 5 | ④ |
| 合计 | 50 | 1.00 | |
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第4组的概率.
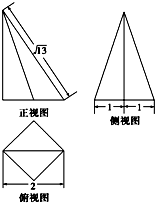 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
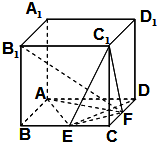 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,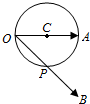 如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.
如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.