题目内容
5.设函数fn(x)=n2x2(1-x)n(n为正整数),则fn(x)在[0,1]上的最大值为( )| A. | 0 | B. | 1 | C. | (1-$\frac{2}{2+n}$)n | D. | 4($\frac{2}{2+n}$)n+2 |
分析 对函数求导,令导数f′(x)=0,解得x的值,分析导函数的符号,确定函数在点x=$\frac{2}{n+2}$取极大值,即函数的最大值,代入函数解析式即可求得结果.
解答 解:f′(x)=2n2x(1-x)n-n×n2x2(1-x)n-1
=n2x(1-x)n-1(2-2x-nx)=-n2x(1-x)n-1[(n+2)x-2]=0
得x=0,或x=1,或x=$\frac{2}{n+2}$
f(x)在(0,$\frac{2}{n+2}$)上单调递增,在($\frac{2}{n+2}$,1)上单调递减,
∴f(x)在[0,1]上的最大值为4($\frac{2}{2+n}$)n+2.
故选:D.
点评 此题考查利用函数的导数研究函数的最值问题,注意导数的运算法则的应用是正确解题的关键,考查运算能力,属中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
15.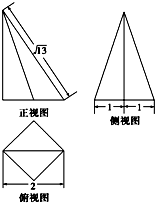 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.i为虚数单位,复平面内表示复数z=$\frac{1}{3+i}$的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.函数y=lg(-x2+2x+8)的增区间为( )
| A. | (-∞,1] | B. | [1,+∞) | C. | (-2,1] | D. | [1,4) |
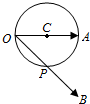 如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.
如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.