题目内容
4．若复数Z满足（2-i）2Z=1（i为虚数单位）．则复数Z的虚部为$\frac{4}{25}$．分析 利用复数的运算法则、虚部的定义即可得出．
解答 解：∵（2-i）2=3-4i，（2-i）2Z=1，
∴Z=$\frac{1}{3-4i}$=$\frac{3+4i}{（3-4i）（3+4i）}$=$\frac{3+4i}{25}$=$\frac{3}{25}+\frac{4i}{25}$，
∴复数Z的虚部为$\frac{4}{25}$，
故答案为：$\frac{4}{25}$．
点评 本题考查了复数的运算法则、虚部的定义，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
14．某校高二年级的一次数学考试中，为了分析学生的得分情况，随机抽取M名同学的成绩，数据的分组统计表如下：
（1）求出表中M，n的值；
（2）为了了解某些同学在数学学习中存在的问题，现从样本中分数在（40，60]中的6位同学中任意抽取2人进行调查，求分数在（40，50]和（50，60]中各有一人的概率．
| 分组 | 频数 | 频率 | 频率/组距 |
| （40，50] | 2 | 0.02 | 0.002 |
| （50，60] | 4 | 0.04 | 0.004 |
| （60，70] | 11 | 0.11 | 0.011 |
| （70，80] | 38 | 0.38 | 0.038 |
| （80，90] | m | n | p |
| （90，100] | 11 | 0.11 | 0.011 |
| 合计 | M | N | P |
（2）为了了解某些同学在数学学习中存在的问题，现从样本中分数在（40，60]中的6位同学中任意抽取2人进行调查，求分数在（40，50]和（50，60]中各有一人的概率．
15．
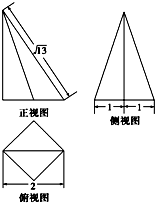某空间几何体的底面为正方形，其三视图如图所示，则该空间几何体的体积等于（ ）
某空间几何体的底面为正方形，其三视图如图所示，则该空间几何体的体积等于（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
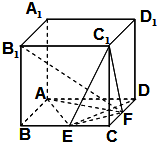如图，在棱长为2的正方体ABCD-A1B1C1D1中，点E，F分别是棱BC，CD的中点，