题目内容
5.设a∈R,函数f(x)=2x2+(x-a)|x-a|,g(x)=lnx;(1)若f(0)=1,试判断y=f[g(x)]在[e,+∞)上的单调性(无需证明);
(2)求f(x)的最小值;
(3)设h(x)=2x2+(3a-2)x-(5a2-7a-3),且x∈(a,+∞),求不等式f(x)>h(x)的解集.
分析 (1)由f(0)=1求出a=-1,从而f(x)=3x2+2x+1,设t=g(x)=lnx,从而函数f[g(x)]是由f(t)和t=lnx复合而成的复合函数,容易说明t=lnx,y=f(t)分别在其定义域[e,+∞),[1,+∞)上单调递增,从而得出函数y=f[g(x)]在[e,+∞)上是增函数;
(2)去绝对值号得到f(x)=$\left\{\begin{array}{l}{3(x-\frac{a}{3})^{2}+\frac{2}{3}{a}^{2}}&{x≥a}\\{(x+a)^{2}-2{a}^{2}}&{x<a}\end{array}\right.$,讨论a≥0和a<0两种情况,然后根据二次函数求最小值,分别求每种情况下x≥a,x<a两段函数上f(x)的最小值,通过比较大小,这样即可求出每种情况下函数f(x)的最小值;
(3)设G(x)=f(x)-h(x)=[x-(2a-3)][x-(3a+1)],x∈(a,+∞),从而看出G(x)=0有两个实数根x=2a-3,和x=3a+1,要解G(x)>0,从而需比较2a-3和3a+1的大小,从而分2a-3<3a+1,2a-3>3a+1,和2a-3=3a+1三种情况对a的取值进行讨论,并且在每种情况下2a-3,3a+1和a进行比较,从而写出G(x)>0即f(x)>g(x)的解.
解答 解:(1)若f(0)=-a|-a|=1,则a=-1;
∴在[e,+∞)上,f(x)=2x2+(x+1)2=3x2+2x+1;
对于函数y=f[g(x)],设t=g(x)=lnx,t≥1;
∴f(t)=3t2+2t+1,t≥1;
而t=lnx在[e,+∞)上单调递增,f(t)在[1,+∞)上单调递增;
∴复合函数y=f[g(x)]在[e,+∞)上单调递增;
(2)记f(x)的最小值为F(a);
f(x)=2x2+(x-a)|x-a|=$\left\{\begin{array}{l}{3(x-\frac{a}{3})^{2}+\frac{2}{3}{a}^{2}}&{x≥a}\\{(x+a)^{2}-2{a}^{2}}&{x<a}\end{array}\right.$;
①当a≥0时,1)若x≥a,f(x)在[a,+∞)上单调递增,∴此时f(x)的最小值为f(a)=2a2;
2)若x<a,x=-a时,f(x)取最小值f(-a)=-2a2;
∴F(a)=-2a2;
②当a<0时,1)若x≥a,f(x)的最小值为$f(\frac{a}{3})=\frac{2}{3}{a}^{2}$;
2)若x<a,f(x)在(-∞,a)上单调递减,∴此时f(x)>f(a)=2a2;
∴$F(a)=\frac{2}{3}{a}^{2}$;
综上得F(a)=$\left\{\begin{array}{l}{-2{a}^{2}}&{a≥0}\\{\frac{2}{3}{a}^{2}}&{a<0}\end{array}\right.$;
(3)设G(x)=f(x)-h(x)=2x2+(x-a)2-2x2-(3a-2)x+(5a2-7a-3)
=x2-(5a-2)x+(6a2-7a-3),x∈(a,+∞);
△=(a+4)2≥0,G(x)=[x-(2a-3)][x-(3a+1)],x∈(a,+∞);
∴①若2a-3<3a+1,即a>-4;
解G(x)>0得,x<2a-3,或x>3a+1;
1)若3a+1<a,即a$<-\frac{1}{2}$,则G(x)>0的解为x>a;
即$-4<a<-\frac{1}{2}$时,f(x)>h(x)的解为x>a;
2)若3a+1≥a,且2a-3<a,即$-\frac{1}{2}≤a<3$,解G(x)>0得x>3a+1;
∴f(x)>g(x)的解为x>3a+1;
3)若2a-3≥a,即a≥3,解G(x)>0得a<x<2a-3,或x>3a+1;
∴f(x)>g(x)的解为a<x<2a-3,或x>3a+1;
②若2a-3>3a+1,即a<-4,2a-3-a=a-3<0;
∴f(x)>g(x)的解为x>a;
③若2a-3=3a+1,即a=-4;
∴f(x)>g(x)的解为x>a;
综上得,1)$a<-\frac{1}{2}$时,f(x)>h(x)的解集为(a,+∞);
2)$-\frac{1}{2}≤a<3$时,f(x)>h(x)的解集为(3a+1,+∞);
3)a≥3时,f(x)>h(x)的解集为(a,2a-3)∪(3a,+1).
点评 考查对数函数,二次函数的单调性,以及复合函数单调性的判断方法,二次函数最值、分段函数最值的求法,以及解一元二次不等式的方法.

 智慧小复习系列答案
智慧小复习系列答案| A. | 21π | B. | 18π | C. | 12π | D. | 9π |
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{{1+\sqrt{5}}}{2}$ |
| 分组 | 频数 | 频率 | 频率/组距 |
| (40,50] | 2 | 0.02 | 0.002 |
| (50,60] | 4 | 0.04 | 0.004 |
| (60,70] | 11 | 0.11 | 0.011 |
| (70,80] | 38 | 0.38 | 0.038 |
| (80,90] | m | n | p |
| (90,100] | 11 | 0.11 | 0.011 |
| 合计 | M | N | P |
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在(40,60]中的6位同学中任意抽取2人进行调查,求分数在(40,50]和(50,60]中各有一人的概率.
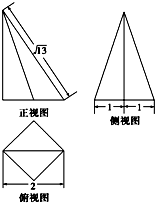 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |