题目内容
10.已知点A($\frac{π}{8}$,f($\frac{π}{8}$))和直线x=$\frac{3π}{8}$分别是函数f(x)=2$\sqrt{2}$sin?xsin(?x+$\frac{π}{4}$)(?>0)相邻的一个对称中心和一条对称轴,将函数f(x)的图象向右平移φ个单位得到函数g(x)的图象,若当x=$\frac{π}{3}$时,g(x)取最大值,则g(x)在[-$\frac{π}{2}$,0]上单调增区间为[-$\frac{π}{6}$,0].分析 由条件利用正弦函数的周期性求得ω的值,再利用三角恒等变换化简f(x)的解析式,结合y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的单调性求得g(x)在[-$\frac{π}{2}$,0]上单调增区间.
解答 解:由题意可得$\frac{T}{4}$=$\frac{1}{4}$•$\frac{2π}{2ω}$=$\frac{3π}{8}$-$\frac{π}{8}$,∴ω=1,
∴f(x)=2$\sqrt{2}$sinxsin(x+$\frac{π}{4}$)=2$\sqrt{2}$sinx($\frac{\sqrt{2}}{2}$sinx+$\frac{\sqrt{2}}{2}$cosx)
=2sin2x+2sinxcosx=1-cos2x+sin2x=1+$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$),
故将函数f(x)的图象向右平移φ个单位得到
函数g(x)=1+$\frac{\sqrt{2}}{2}$sin[2(x-φ)-$\frac{π}{4}$]=1+$\frac{\sqrt{2}}{2}$sin(2x-2φ-$\frac{π}{4}$)的图象.
由于当x=$\frac{π}{3}$时,g(x)取最大值,即 1+$\frac{\sqrt{2}}{2}$sin($\frac{2π}{3}$-2φ-$\frac{π}{4}$)=1+$\frac{\sqrt{2}}{2}$,
∴$\frac{2π}{3}$-2φ-$\frac{π}{4}$=2kπ+$\frac{π}{2}$,k∈z,
求得φ=-kπ-$\frac{π}{24}$,k∈z,
故可取φ=-$\frac{π}{24}$,g(x)=1+$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{6}$).
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得 kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,
故函数g(x)的增区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈z.
再结合x∈[-$\frac{π}{2}$,0],可得g(x)的增区间为[-$\frac{π}{6}$,0],
故答案为:[-$\frac{π}{6}$,0].
点评 本题主要考查三角恒等变换,y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性、单调性,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 21π | B. | 18π | C. | 12π | D. | 9π |
| 组序 | 高度区间 | 频数 | 频率 |
| 1 | [230,235) | 8 | 0.16 |
| 2 | [235,240) | ① | 0.24 |
| 3 | [240,245) | ② | 0.20 |
| 4 | [245,250) | 10 | ③ |
| 5 | [250,255] | 5 | ④ |
| 合计 | 50 | 1.00 | |
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第4组的概率.
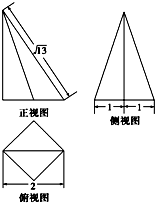 某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )
某空间几何体的底面为正方形,其三视图如图所示,则该空间几何体的体积等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
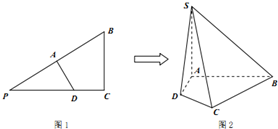 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.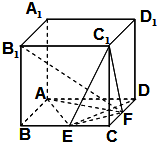 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,