题目内容
已知抛物线C的顶点在原点,焦点为F(2, 0)。
(1)求抛物线C的方程;
(2)过 的直线
的直线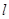 交曲线
交曲线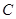 于
于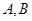 两点,又
两点,又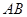 的中垂线交
的中垂线交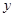 轴于点
轴于点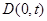 ,
,
求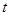 的取值范围。
的取值范围。
(1)求抛物线C的方程;
(2)过
 的直线
的直线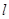 交曲线
交曲线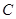 于
于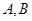 两点,又
两点,又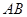 的中垂线交
的中垂线交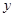 轴于点
轴于点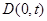 ,
,求
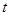 的取值范围。
的取值范围。 (1)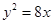 (2)
(2)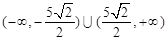
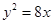 (2)
(2)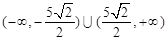
本试题主要考查而来抛物线的方程,以及直线啊你与抛物线的位置关系的运用。
解:(1)设抛物线方程为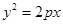 ,则
,则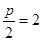 ,
,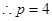
所以,抛物线的方程是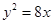 . …………………4分
. …………………4分
(2)直线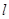 的方程是
的方程是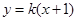 ,联立
,联立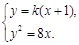 消去
消去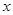 得
得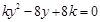 ,…6分
,…6分
显然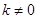 ,由
,由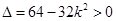 ,得
,得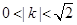 . ……………8分
. ……………8分
由韦达定理得,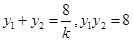 ,
,
所以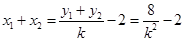 ,则
,则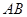 中点
中点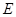 坐标是
坐标是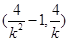 ,……10分
,……10分
由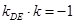 可得
可得 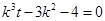 ,
,
所以,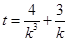 ,令
,令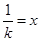 ,则
,则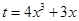 ,其中
,其中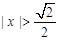 ,…………12分
,…………12分
因为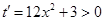 ,所以函数
,所以函数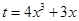 是在
是在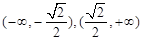 上增函数.
上增函数.
所以,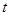 的取值范围是
的取值范围是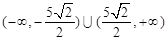
解:(1)设抛物线方程为
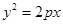 ,则
,则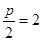 ,
,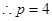
所以,抛物线的方程是
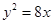 . …………………4分
. …………………4分(2)直线
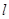 的方程是
的方程是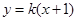 ,联立
,联立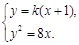 消去
消去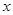 得
得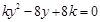 ,…6分
,…6分显然
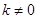 ,由
,由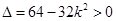 ,得
,得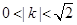 . ……………8分
. ……………8分由韦达定理得,
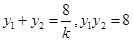 ,
,所以
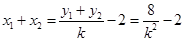 ,则
,则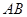 中点
中点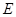 坐标是
坐标是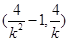 ,……10分
,……10分由
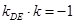 可得
可得 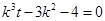 ,
, 所以,
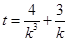 ,令
,令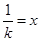 ,则
,则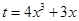 ,其中
,其中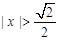 ,…………12分
,…………12分因为
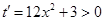 ,所以函数
,所以函数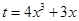 是在
是在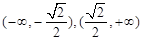 上增函数.
上增函数.所以,
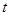 的取值范围是
的取值范围是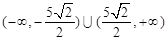

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 中,椭圆
中,椭圆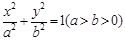 的左、右焦点分别为
的左、右焦点分别为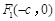 ,
,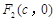 .已知
.已知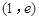 和
和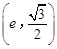 都在椭圆上,其中
都在椭圆上,其中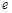 为椭圆的离心率.
为椭圆的离心率.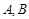 是椭圆上位于
是椭圆上位于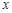 轴上方的两点,且直线
轴上方的两点,且直线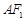 与直线
与直线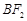 平行,
平行,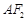 与
与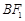 交于点P.
交于点P.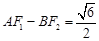 ,求直线
,求直线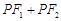 是定值.
是定值.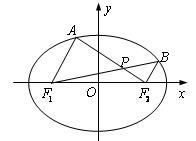
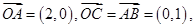 动点
动点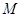 到定直线
到定直线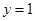 的距离等于
的距离等于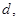 并且满足
并且满足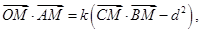 其中
其中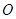 是坐标原点,
是坐标原点,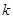 是参数.
是参数.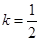 时,求
时,求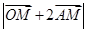 的最大值和最小值;
的最大值和最小值;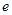 满足
满足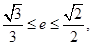 求实数
求实数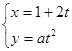 ,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。
,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。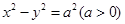 的左、右顶点分别为
的左、右顶点分别为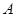 、
、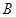 ,点
,点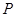 是第一象限内双曲线上的点.若直线
是第一象限内双曲线上的点.若直线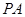 、
、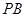 的倾斜角分别为
的倾斜角分别为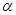 ,
,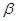 ,且
,且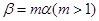 ,那么
,那么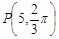 ,
, 为极点,求使
为极点,求使 是正三角形的
是正三角形的 点的极坐标为_______ __
点的极坐标为_______ __
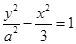 的两个焦点分别为
的两个焦点分别为 、
、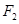 ,离心率为2.
,离心率为2.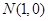 能否作出直线
能否作出直线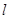 ,使
,使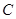 交于
交于 、
、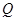 两点,且
两点,且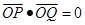 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.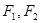 是双曲线
是双曲线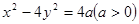 的两个焦点,点
的两个焦点,点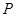 在双曲线上,且满足:
在双曲线上,且满足: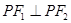 ,
,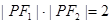 ,则
,则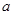 的值为( )
的值为( )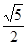
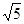
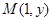 在抛物线
在抛物线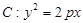
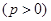 上,
上,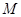 点到抛物线
点到抛物线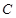 的焦点F的距离为2.
的焦点F的距离为2. 与抛物线C交于O (坐标原点),A两点,直线
与抛物线C交于O (坐标原点),A两点,直线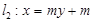 与抛物线C交于B,D两点.
与抛物线C交于B,D两点. 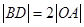 ,求实数
,求实数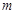 的值;
的值;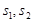 分别为三角形OAA1和四边形BB1D1D的面积,求
分别为三角形OAA1和四边形BB1D1D的面积,求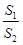 的取值范围.
的取值范围.