题目内容
设双曲线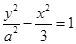 的两个焦点分别为
的两个焦点分别为 、
、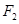 ,离心率为2.
,离心率为2.
(1)求双曲线的渐近线方程;
(2)过点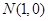 能否作出直线
能否作出直线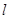 ,使
,使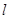 与双曲线
与双曲线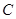 交于
交于 、
、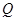 两点,且
两点,且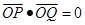 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.
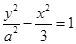 的两个焦点分别为
的两个焦点分别为 、
、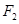 ,离心率为2.
,离心率为2.(1)求双曲线的渐近线方程;
(2)过点
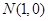 能否作出直线
能否作出直线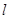 ,使
,使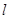 与双曲线
与双曲线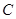 交于
交于 、
、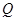 两点,且
两点,且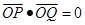 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.(1)∵ 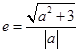 ∴
∴ 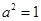 ∴ 双曲线渐近线方程为
∴ 双曲线渐近线方程为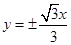
(2)解:假设过点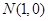 能作出直线
能作出直线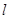 ,使
,使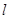 与双曲线
与双曲线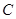 交于
交于 、
、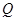 两点,
两点,
且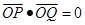 若过点
若过点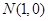 的直线斜率不存在,则不适合题意,舍去.
的直线斜率不存在,则不适合题意,舍去.
设直线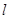 方程为
方程为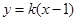
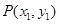
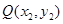
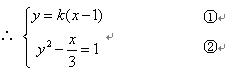
①代入②得: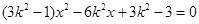
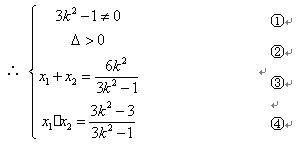
∵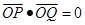 ∴
∴ 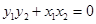 ∴
∴ 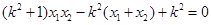
∴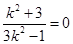 ∴
∴ 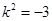 不合题意. ∴ 不存在这样的直线.
不合题意. ∴ 不存在这样的直线.
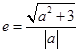 ∴
∴ 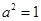 ∴ 双曲线渐近线方程为
∴ 双曲线渐近线方程为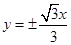
(2)解:假设过点
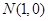 能作出直线
能作出直线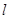 ,使
,使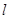 与双曲线
与双曲线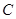 交于
交于 、
、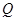 两点,
两点,且
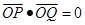 若过点
若过点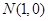 的直线斜率不存在,则不适合题意,舍去.
的直线斜率不存在,则不适合题意,舍去.设直线
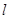 方程为
方程为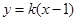
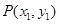
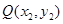
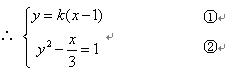
①代入②得:
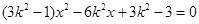
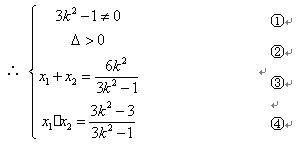
∵
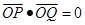 ∴
∴ 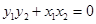 ∴
∴ 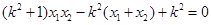
∴
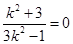 ∴
∴ 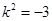 不合题意. ∴ 不存在这样的直线.
不合题意. ∴ 不存在这样的直线.(1)根据离心率先求出a2的值,然后令双曲线等于右侧的1为0,解此方程可得双曲线的渐近线方程.
(2)设直线l的方程为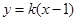 ,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理
,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理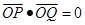 表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
(2)设直线l的方程为
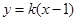 ,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理
,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理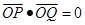 表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
练习册系列答案
相关题目
 为圆
为圆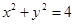 上的动点,且
上的动点,且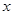 轴上,
轴上,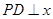 轴,垂足为
轴,垂足为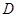 ,线段
,线段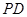 中点
中点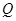 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点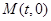
 任作一条与
任作一条与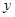 轴不垂直的直线
轴不垂直的直线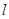 ,它与曲线
,它与曲线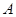 、
、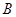 两点。
两点。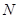 ,使得
,使得 总能被
总能被 的左右焦点,过F1的直线与左支交于A、B两点,若
的左右焦点,过F1的直线与左支交于A、B两点,若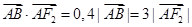 ,则该双曲线的离心率是为( )
,则该双曲线的离心率是为( ) B.
B. C.
C.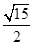 D.
D.
 的直线
的直线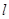 交曲线
交曲线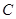 于
于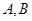 两点,又
两点,又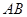 的中垂线交
的中垂线交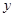 轴于点
轴于点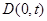 ,
,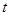 的取值范围。
的取值范围。 倍后得到点Q(x,
倍后得到点Q(x,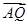 ·
·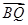 =1.
=1. 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且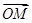 +
+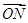 +
+ =
=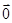 ,试求△MNH的面积.
,试求△MNH的面积.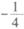 ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C. 与曲线C交于P,Q两点,若
与曲线C交于P,Q两点,若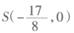 ,证明:
,证明: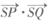 为定值.
为定值.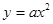 在点(1,
在点(1,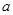 )处的切线与直线
)处的切线与直线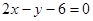 平行,则
平行,则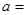 ( )
( )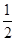
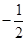
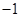
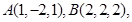 点
点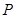 在
在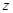 轴上,且
轴上,且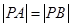 ,则点
,则点 的坐标分别是
的坐标分别是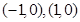 ,直线
,直线 相交于点
相交于点 ,且直线
,且直线 与直线
与直线 的斜率之差是
的斜率之差是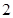 ,则点
,则点


