题目内容
已知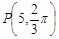 ,
, 为极点,求使
为极点,求使 是正三角形的
是正三角形的 点的极坐标为_______ __
点的极坐标为_______ __
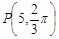 ,
, 为极点,求使
为极点,求使 是正三角形的
是正三角形的 点的极坐标为_______ __
点的极坐标为_______ __
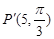 或
或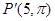
解:P的直角坐标为 (5cos2π/ 3 ,5sin2π /3 ),即 (-5 /2 ,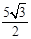 ).当△POP′是正三角形时,设P(m,n ),则∠POP′=60°,OP=OP′=
).当△POP′是正三角形时,设P(m,n ),则∠POP′=60°,OP=OP′= 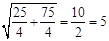 故有
故有
tan60°=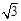 ="|[n/" m -(-
="|[n/" m -(-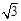 ) ]/ [1+n /m •(-
) ]/ [1+n /m •(-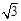 )] | ①,且
)] | ①,且 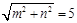 ②.
②.
由①②解得 m="-5" 且n=0,或 m="5" /2 ,n=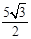 ,即P(-5,0),或 P( 5 /2 ,
,即P(-5,0),或 P( 5 /2 ,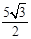 ),
),
根据ρ= m2+n2 和 tanθ="n/" m ,求得P′的极坐标(ρ,θ ).
故P′点的极坐标为(5,π)或(5,π /3 ),故答案为 (5,π)或(5,π /3 ).
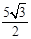 ).当△POP′是正三角形时,设P(m,n ),则∠POP′=60°,OP=OP′=
).当△POP′是正三角形时,设P(m,n ),则∠POP′=60°,OP=OP′= 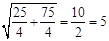 故有
故有tan60°=
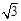 ="|[n/" m -(-
="|[n/" m -(-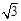 ) ]/ [1+n /m •(-
) ]/ [1+n /m •(-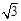 )] | ①,且
)] | ①,且 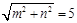 ②.
②.由①②解得 m="-5" 且n=0,或 m="5" /2 ,n=
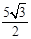 ,即P(-5,0),或 P( 5 /2 ,
,即P(-5,0),或 P( 5 /2 ,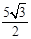 ),
),根据ρ= m2+n2 和 tanθ="n/" m ,求得P′的极坐标(ρ,θ ).
故P′点的极坐标为(5,π)或(5,π /3 ),故答案为 (5,π)或(5,π /3 ).

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 为圆
为圆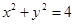 上的动点,且
上的动点,且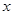 轴上,
轴上,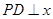 轴,垂足为
轴,垂足为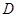 ,线段
,线段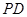 中点
中点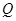 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点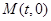
 任作一条与
任作一条与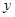 轴不垂直的直线
轴不垂直的直线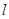 ,它与曲线
,它与曲线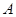 、
、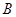 两点。
两点。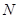 ,使得
,使得 总能被
总能被 ,直线AM,BM相交于点M,且它们的斜率之和是2,则点M的轨迹方程是( )
,直线AM,BM相交于点M,且它们的斜率之和是2,则点M的轨迹方程是( )



 •
• 的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.
的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.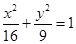 的左、右焦点分别为
的左、右焦点分别为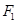 、
、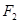 , 过焦点F1的直线交椭圆于
, 过焦点F1的直线交椭圆于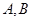 两点,若
两点,若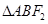 的内切圆的面积为
的内切圆的面积为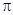 ,
,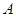 ,
,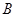 两点的坐标分别为
两点的坐标分别为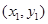 和
和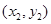 ,则
,则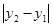 的值为___________。
的值为___________。 的直线
的直线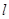 交曲线
交曲线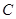 于
于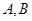 两点,又
两点,又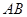 的中垂线交
的中垂线交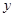 轴于点
轴于点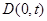 ,
,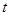 的取值范围。
的取值范围。 倍后得到点Q(x,
倍后得到点Q(x,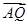 ·
·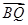 =1.
=1. 的直线l交曲线C于M、N两点,且
的直线l交曲线C于M、N两点,且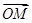 +
+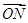 +
+ =
=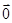 ,试求△MNH的面积.
,试求△MNH的面积.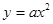 在点(1,
在点(1,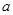 )处的切线与直线
)处的切线与直线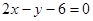 平行,则
平行,则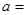 ( )
( )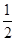
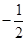
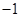
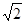 +1,
+1,