题目内容
如图,在平面直角坐标系 中,椭圆
中,椭圆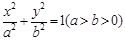 的左、右焦点分别为
的左、右焦点分别为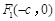 ,
,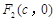 .已知
.已知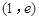 和
和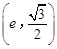 都在椭圆上,其中
都在椭圆上,其中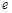 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
(2)设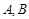 是椭圆上位于
是椭圆上位于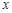 轴上方的两点,且直线
轴上方的两点,且直线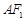 与直线
与直线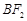 平行,
平行,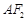 与
与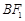 交于点P.
交于点P.
(i)若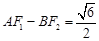 ,求直线
,求直线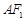 的斜率;
的斜率;
(ii)求证: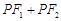 是定值.
是定值.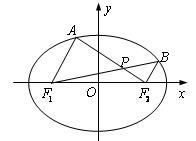
 中,椭圆
中,椭圆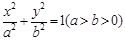 的左、右焦点分别为
的左、右焦点分别为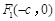 ,
,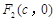 .已知
.已知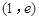 和
和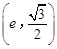 都在椭圆上,其中
都在椭圆上,其中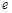 为椭圆的离心率.
为椭圆的离心率.(1)求椭圆的方程;
(2)设
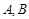 是椭圆上位于
是椭圆上位于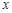 轴上方的两点,且直线
轴上方的两点,且直线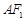 与直线
与直线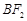 平行,
平行,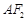 与
与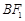 交于点P.
交于点P.(i)若
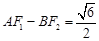 ,求直线
,求直线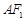 的斜率;
的斜率;(ii)求证:
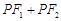 是定值.
是定值.
见解析
【考点】椭圆的性质,直线方程,两点间的距离公式。
【考点】椭圆的性质,直线方程,两点间的距离公式。
(1)根据椭圆的性质和已知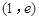 和
和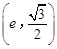 都在椭圆上列式求解。
都在椭圆上列式求解。
(2)根据已知条件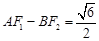 ,用待定系数法求解
,用待定系数法求解
解:(1)由题设知,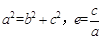 ,由点
,由点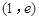 在椭圆上,得
在椭圆上,得
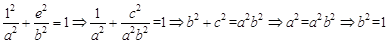 ,∴
,∴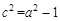 。
。
由点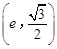 在椭圆上,得
在椭圆上,得
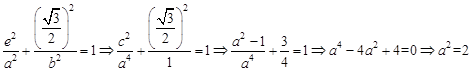
∴椭圆的方程为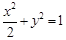 。
。
(2)由(1)得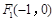 ,
,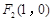 ,又∵
,又∵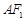 ∥
∥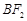 ,
,
∴设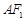 、
、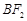 的方程分别为
的方程分别为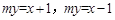 ,
,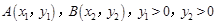 。
。
∴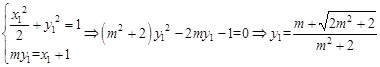 。
。
∴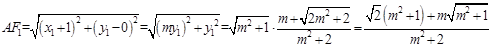 。①
。①
同理,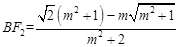 。②
。②
(i)由①②得,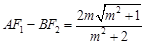 。解
。解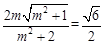 得
得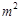 =2。
=2。
∵注意到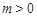 ,∴
,∴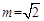 。
。
∴直线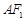 的斜率为
的斜率为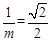 。
。
(ii)证明:∵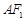 ∥
∥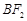 ,∴
,∴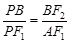 ,即
,即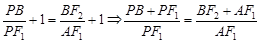 。
。
∴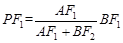 。
。
由点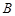 在椭圆上知,
在椭圆上知,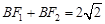 ,∴
,∴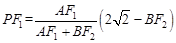 。
。
同理。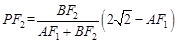 。
。
∴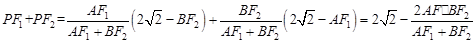
由①②得,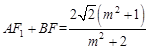 ,
,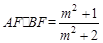 ,
,
∴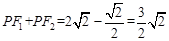 。
。
∴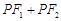 是定值。
是定值。
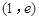 和
和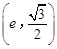 都在椭圆上列式求解。
都在椭圆上列式求解。(2)根据已知条件
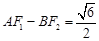 ,用待定系数法求解
,用待定系数法求解解:(1)由题设知,
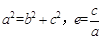 ,由点
,由点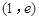 在椭圆上,得
在椭圆上,得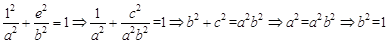 ,∴
,∴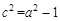 。
。由点
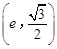 在椭圆上,得
在椭圆上,得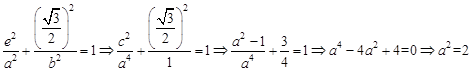
∴椭圆的方程为
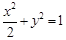 。
。(2)由(1)得
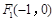 ,
,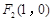 ,又∵
,又∵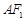 ∥
∥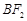 ,
,∴设
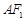 、
、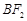 的方程分别为
的方程分别为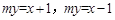 ,
,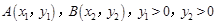 。
。∴
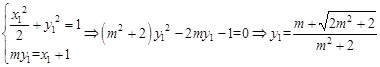 。
。∴
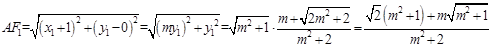 。①
。①同理,
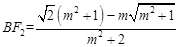 。②
。②(i)由①②得,
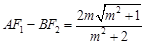 。解
。解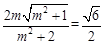 得
得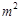 =2。
=2。∵注意到
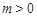 ,∴
,∴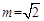 。
。∴直线
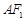 的斜率为
的斜率为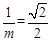 。
。(ii)证明:∵
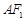 ∥
∥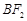 ,∴
,∴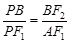 ,即
,即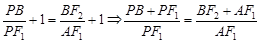 。
。∴
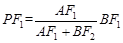 。
。由点
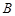 在椭圆上知,
在椭圆上知,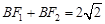 ,∴
,∴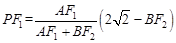 。
。同理。
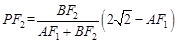 。
。∴
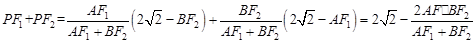
由①②得,
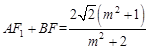 ,
,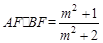 ,
,∴
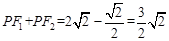 。
。∴
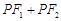 是定值。
是定值。
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 为圆
为圆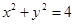 上的动点,且
上的动点,且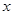 轴上,
轴上,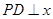 轴,垂足为
轴,垂足为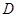 ,线段
,线段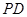 中点
中点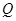 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点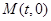
 任作一条与
任作一条与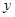 轴不垂直的直线
轴不垂直的直线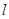 ,它与曲线
,它与曲线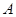 、
、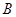 两点。
两点。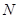 ,使得
,使得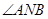 总能被
总能被 ;
;
 轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
轴的正半轴的交点,求四边形OADB的最大面积及D点坐标. 、
、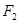 在x轴上,离心率
在x轴上,离心率
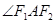 的角平分线所在直线
的角平分线所在直线 的方程.
的方程.
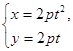 (t为参数),其中p>0,焦点为F,准线为
(t为参数),其中p>0,焦点为F,准线为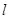 . 过抛物线上一点M作
. 过抛物线上一点M作 的直线
的直线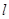 交曲线
交曲线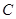 于
于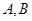 两点,又
两点,又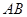 的中垂线交
的中垂线交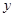 轴于点
轴于点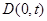 ,
,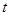 的取值范围。
的取值范围。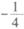 ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C. 与曲线C交于P,Q两点,若
与曲线C交于P,Q两点,若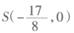 ,证明:
,证明: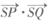 为定值.
为定值. |=2,O为AB中点,直线
|=2,O为AB中点,直线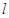 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与
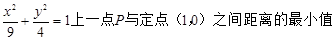 ( )。
( )。