题目内容
10.如图,在等腰梯形CDFE中,A,B分别为底边DF,CE的中点,AD=2AB=2BC=2.沿AE将△AEF折起,使二面角F-AE-C为直二面角,连接CF、DF.(Ⅰ)证明:平面ACF⊥平面AEF;
(Ⅱ)求点D到平面ACF的距离.

分析 (Ⅰ)证明EF⊥EA;EF⊥AC;推出平面AEF⊥平面AECD,得到AC⊥EF,AC⊥AE,证明AC⊥平面AEF,然后证明平面ACF⊥平面AEF.
(Ⅱ)点D到平面ACF的距离即三棱锥D-ACF的高,利用VD-ACV=VV-ACD求解即可.
解答 解:(Ⅰ)在等腰梯形CSFE中,由已知条件可得,
CD=AC=AE=EF=$\sqrt{2}$,AF=AD=2,
所以,AE2+EF2=AF2,∴EF⊥EA;同理可证,EF⊥AC;…(2分)
在四棱锥F-AECD中,
∵二面角F-AE-C为直二面角,
∴平面AEF⊥平面AECD,
∴EF⊥平面AECD,…(4分)
∵AC?平面AECD,
∴AC⊥EF,又∵AC⊥AE,
∴AC⊥平面AEF,
∴平面ACF⊥平面AEF.…(6分)
(Ⅱ)点D到平面ACF的距离即三棱锥D-ACF的高,
所以VD-ACV=VV-ACD ….(8分)
因为AB=BC=1,所以AC=$\sqrt{2}$,AF=2且AC⊥AF,
所以S△ACV=$\frac{1}{2}$×$\sqrt{2}×2$=$\sqrt{2}$.
又因为AC=CD=$\sqrt{2}$且AC⊥CD,
所以S△ACD=$\frac{1}{2}±\sqrt{2}×\sqrt{2}=1$,$EF=\sqrt{2}$….(10分)
所以$\frac{1}{3}×\sqrt{2}×d=\frac{1}{3}×1×\sqrt{2}$ 即
d=1….(12分)
点评 本题看直线与平面垂直,平面与平面垂直的判定定理的应用,曹休墓距离的应用,考查逻辑推理能力以及计算能力.

练习册系列答案
相关题目
20.下列说法:
①设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为$\stackrel{∧}{y}$=0.85x-85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg;
②命题“?x≥1,x2+3≥4”的否定是“?x<1,x2+3<4”
③相关系数r越小,表明两个变量相关性越弱;
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握认为这两个变量间有关系;
⑤已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤5)=0.79,则P(ξ≤-1)=0.21;
其中错误的个数是( )
本题可参考独立性检验临界值表:
①设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为$\stackrel{∧}{y}$=0.85x-85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg;
②命题“?x≥1,x2+3≥4”的否定是“?x<1,x2+3<4”
③相关系数r越小,表明两个变量相关性越弱;
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握认为这两个变量间有关系;
⑤已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤5)=0.79,则P(ξ≤-1)=0.21;
其中错误的个数是( )
本题可参考独立性检验临界值表:
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.已知命题p:?x0∈R,x02+2x0+1≤0,则¬p为( )
| A. | ?x0∈R,x02+2x0+1>0 | B. | ?x∈R,x2+2x+1≤0 | ||
| C. | ?x∈R,x2+2x+1≥0 | D. | ?x∈R,x2+2x+1>0 |
18.函数y=cos2(x+$\frac{π}{2}$)的单调递增区间( )
| A. | (kπ,kπ+$\frac{π}{2}$)k∈Z | B. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z | C. | (2kπ,2kπ+π)k∈Z | D. | (2kπ,2kπ+2π)k∈Z |
5.小王参加网购后,快递员电话通知于本周五早上7:30-8:30送货到家,如果小王这一天离开家的时间为早上8:00-9:00,那么在他走之前拿到邮件的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{8}$ |
15.已知F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,a为双曲线虚轴的一个顶点,过点F、A的直线与双曲线的一条渐近线在y轴右侧的交点为B,若$\overrightarrow{AB}$=($\sqrt{2}$-1)$\overrightarrow{AF}$,则此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
2.设集合A={x∈N|y=ln(2-x)},B={x|x(x-1)≤0},则A∩B=( )
| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {1} | D. | {0,1} |
19.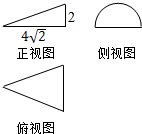 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )| A. | $\frac{8\sqrt{2}π}{3}$ | B. | $\frac{16\sqrt{2}π}{3}$ | C. | 4$\sqrt{2}π$ | D. | 8$\sqrt{2}π$ |
20.已知集合 A={x∈R|x-1≥0},B={x∈R||x|≤2},则A∩B=( )
| A. | {x∈R|-2≤x≤2} | B. | {x∈R|-1≤x≤2} | C. | {x∈R|1≤x≤2} | D. | {x∈R|-1≤x≤1} |