题目内容
14．
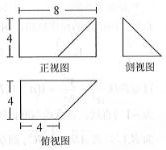已知某几何体的三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，则该几何体的体积为$\frac{160}{3}$．
分析 由已知中的三视图，可知该几何体是一个三棱柱切去一个三棱锥所得的组合体，分别求出体积后，相减可得答案．
解答 解：由已知中的三视图，可知该几何体是一个三棱柱切去一个三棱锥所得的组合体，
棱柱和棱锥的底面均为侧视图，
故底面面积S=$\frac{1}{2}$×4×4=8，
棱柱的高为8，故体积为64，
棱锥的高为4，故体积为：$\frac{32}{3}$，
故组合体的体积V=64-$\frac{32}{3}$=$\frac{160}{3}$，
故答案为：$\frac{160}{3}$
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
5．小王参加网购后，快递员电话通知于本周五早上7：30-8：30送货到家，如果小王这一天离开家的时间为早上8：00-9：00，那么在他走之前拿到邮件的概率为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{7}{8}$ |
2．设集合A={x∈N|y=ln（2-x）}，B={x|x（x-1）≤0}，则A∩B=（ ）
| A． | {x|x≥1} | B． | {x|1≤x＜2} | C． | {1} | D． | {0，1} |
9．一个几何体的三视图如图所示，其中左视图为直角三角形，则该几何体的体积为（ ）
| A． | 16$\sqrt{2}$ | B． | $\frac{{4\sqrt{2}}}{3}$ | C． | $\frac{{8\sqrt{2}}}{3}$ | D． | $\frac{{16\sqrt{2}}}{3}$ |
19．
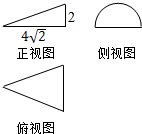一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（ ）
一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（ ）| A． | $\frac{8\sqrt{2}π}{3}$ | B． | $\frac{16\sqrt{2}π}{3}$ | C． | 4$\sqrt{2}π$ | D． | 8$\sqrt{2}π$ |
4．已知互不相等的正数a，b，c，d，p，q满足a，c，b，d成等差数列，a，p，b，q成等比数列，则（ ）
| A． | c＜p，d＞q | B． | c＞p，d＞q | C． | c＞p，d＜q | D． | c＜p，d＜q |