题目内容
15.如图△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,AD=3,则BD的长为( )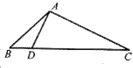
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 通过诱导公式易知cos∠BAD=$\frac{2\sqrt{2}}{3}$,利用余弦定理计算即得结论.
解答 解:∵AD⊥AC,∴∠DAC=90°,
∴sin∠BAC=sin(∠BAD+90°)=cos∠BAD=$\frac{2\sqrt{2}}{3}$,
又∵AB=3$\sqrt{2}$,AD=3,
∴BD2=AB2+AD2-2AB•ADcos∠BAD
=18+9-$2×3\sqrt{2}×3×\frac{2\sqrt{2}}{3}$
=3,
∴BD=$\sqrt{3}$,
故选:C.
点评 本题考查求三角形中某条线段的长度,利用三角函数的诱导公式、余弦定理是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
6.执行如图的程序框图,如果输入的a=log32,b=log52,c=log23,那么输出m的值是( )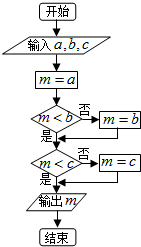

| A. | log52 | B. | log32 | C. | log23 | D. | 都有可能 |
20.下列说法:
①设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为$\stackrel{∧}{y}$=0.85x-85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg;
②命题“?x≥1,x2+3≥4”的否定是“?x<1,x2+3<4”
③相关系数r越小,表明两个变量相关性越弱;
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握认为这两个变量间有关系;
⑤已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤5)=0.79,则P(ξ≤-1)=0.21;
其中错误的个数是( )
本题可参考独立性检验临界值表:
①设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为$\stackrel{∧}{y}$=0.85x-85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg;
②命题“?x≥1,x2+3≥4”的否定是“?x<1,x2+3<4”
③相关系数r越小,表明两个变量相关性越弱;
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握认为这两个变量间有关系;
⑤已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤5)=0.79,则P(ξ≤-1)=0.21;
其中错误的个数是( )
本题可参考独立性检验临界值表:
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.小王参加网购后,快递员电话通知于本周五早上7:30-8:30送货到家,如果小王这一天离开家的时间为早上8:00-9:00,那么在他走之前拿到邮件的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{8}$ |