题目内容
4.(x-$\frac{2}{x}$)8的二项展开式中,常数项为1120.分析 利用二项展开式的通项公式求出二项展开式的第r+1项,令x的指数为0得常数项.
解答 解:展开式的通项公式为Tr+1=(-2)rC8rx8-2r
令8-2r=0得r=4
得常数项为C84(-2)4=1120.
故答案为:1120.
点评 二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
14.已知复数z=$\frac{a+i}{1-i}$(a∈R)为纯虚数,则a=( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
16.已知条件p:x>1,q:$\frac{1}{x}$<1,则¬p是¬q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.针对时下的网购热,某单位对“喜欢网购与职工性别是否有关”进行了一次调查,其中男职工有60人,女职工人数是男职工人数的$\frac{1}{2}$,喜欢网购的男职工人数是男职工人数的$\frac{1}{6}$,喜欢网购的女职工人数是女职工人数的$\frac{2}{3}$.
(1)根据以上数据完成下面的2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为喜欢网购与职工性别有关系?
参考数据及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(1)根据以上数据完成下面的2×2列联表.
| 喜欢网购 | 不喜欢网购 | 总计 | |
| 男职工 | |||
| 女职工 | |||
| 总计 |
参考数据及公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
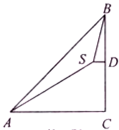 如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.