题目内容
9.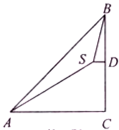 如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
分析 作出图形,过点S作SE⊥AC于E,SH⊥AB于H,依题意可求得SE在△BDS中利用正弦定理可求BD的长,从而可得山顶高BC.
解答 解:依题意,过S点作SE⊥AC于E,SH⊥AB于H,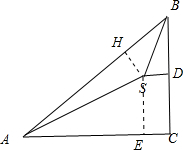 ∵∠SAE=30°,AS=2000米,
∵∠SAE=30°,AS=2000米,
∴CD=SE=AS•sin30°=1000米,
依题意,在Rt△HAS中,∠HAS=45°-30°=15°,
∴HS=AS•sin15°,
在Rt△BHS中,∠HBS=30°,
∴BS=2HS=4000sin15°,
在Rt△BSD中,
BD=BS•sin75°
=4000sin15°•sin75°
=4000sin15°•cos15°
=2000×sin30°
=1000米.
∴BC=BD+CD=1000+1000=2000米;
故答案为:2000.
点评 本题考查正弦定理的应用,考查作图与计算的能力,关键是将实际问题转化为数学问题中的解三角形的问题解答;属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知函数f(x)=lnx-x(0<x<1),则下列不等式正确的是( )
| A. | f2(x)<f(x2)<f(x) | B. | f(x2)<f2(x)<f(x) | C. | f(x)<f(x2)<f2(x) | D. | f(x2)<f(x)<f2(x) |
20.已知函数y=f(x+2)的图象关于直线x=-2对称,且当x∈(-∞,0)时,f(x)+xf′(x)>0成立.若a=(20.2)•f(20.2),b=(ln2)•f(ln2),c=(log24)•f(log24),则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
1.在下列四个函数中,在(0,+∞)为增函数的是( )
| A. | y=3-x | B. | y=x2-3x | C. | $f(x)={(\frac{1}{2})^x}$ | D. | f(x)=|x| |
19.某校高一年级有200人,其中100人参加数学第二课堂活动.在期末考试中,分别对参加数学第二课堂活动的同学与未参加数学第二课堂活动的同学的数学成绩进行调查.按照学生数学成绩优秀与非优秀人数统计后,构成如下不完整的2×2列联表:
已知p是(1+2x)5展开式中的第三项系数,q是(1+2x)5展开式中的第四项的二项式系数.
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
| 优秀 | 非优秀 | 总计 | |
| 参加数学第二课堂活动 | p | ||
| 未参加数学第二课堂活动 | q | 100 | |
| 总计 | 200 |
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
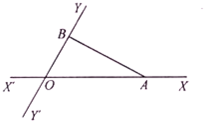 如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.
如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.