Question

【题目】如图，已知直线l1：kx+y=0和直线l2：kx+y+b=0（b＞0），射线OC的一个法向量为 =（﹣k，1），点O为坐标原点，且k≥0，直线l1和l2之间的距离为2，点A、B分别是直线l1、l2上的动点，P（4，2），PM⊥l1于点M，PN⊥OC于点N；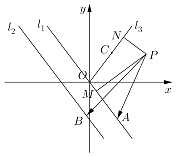

（1）若k=1，求|OM|+|ON|的值；
（2）若| |=8，求 的最大值；
（3）若k=0，AB⊥l2 ， 且Q（﹣4，﹣4），试求|PA|+|AB|+|BQ|的最小值．

Answer 1

【答案】
（1）解：∵k=1．

∴射线OC的一个法向量为 =（﹣1，1），

∴射线OC的斜率为1，射线OC的方程为：y=x（x≥0）．

∴|PN|= = ，|OP|= =2 ，

∴|ON|= =3 ．

直线l1：x+y=0，|PM|= =3 ，

∴|OM|= = ．

∴|OM|+|ON|=4

（2）解：k≥0，b＞0，直线l1和l2之间的距离为2，

∴ =2，化为：b2=4（k2+1）．

设A（m，﹣km），B（n，﹣kn﹣b）．

∵P（4，2），| |=8，

∴ =（m+n﹣8，﹣km﹣kn﹣b﹣4），

则（m+n﹣8）2+（km+kn+b+4）2=64≥2（m﹣4）（n﹣4）+2（km+2）（kn+b+2），

=（m﹣4）（n﹣4）+（﹣km﹣2）（﹣kn﹣b﹣2）

=（m﹣4）（n﹣4）+（km+2）（kn+b+2）≤32，

故 的最大值为32

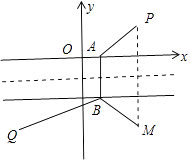
（3）解：k=0，直线l1：y=0，直线l2：y+2=0，如图所示．

作出点P关于直线y=﹣1的对称点M（4，﹣4），则|PA|=|BM|．

设B（x，﹣2）．

∴|PA|+|AB|+|BQ|=|BM|+|QB|+2

= + +2，

同理由对称性可得：当且仅当B取点（0，﹣2）时，

|BM|+|QB|取得最小值2 =4 ．

∴|PA|+|AB|+|BQ|的最小值为4 +2．

【解析】（1）若k=1，则可得|OM|= ．|ON|=3 ，进而得到|OM|+|ON|的值；（2）若| |=8，利用柯西不等式可得 ≤32；（3）若k=0，AB⊥l2 ， 且Q（﹣4，﹣4），|PA|+|AB|+|BQ|=|BM|+|QB|+2，当且仅当B取点（0，﹣2）时，|BM|+|QB|取得最小值．