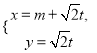题目内容
【题目】【选修4—4:坐标系与参数方程】
将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线![]() 与C的交点为
与C的交点为![]() ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
【答案】(Ⅰ)![]() 得参数方程为
得参数方程为![]() (
(![]() 为参数) (II)
为参数) (II)![]()
【解析】试题分析:(1)根据变换得![]() ,再利用三角换元得
,再利用三角换元得![]() (2)先求出直角坐标方程:由直线方程与椭圆方程解得交点坐标P1(2,0),P2(0,1),得中点坐标
(2)先求出直角坐标方程:由直线方程与椭圆方程解得交点坐标P1(2,0),P2(0,1),得中点坐标![]() ,利用点斜式得直线方程
,利用点斜式得直线方程![]() ,最后根据
,最后根据![]() 得极坐标方程
得极坐标方程
试题解析:(I)设(x1,y1)为圆上的点,在已知变换下变为C上点(x,y),
依题意得:圆![]() 的参数方程为
的参数方程为![]() (t为参数)
(t为参数)
所以C的参数方程为![]() (t为参数).
(t为参数).
(II)由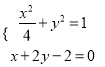 解得
解得![]() 或
或![]()
所以P1(2,0),P2(0,1),则线段P1P2的中点坐标为![]() ,所求直线的斜率k=
,所求直线的斜率k=![]() ,于是所求直线方程为
,于是所求直线方程为![]() ,并整理得
,并整理得![]()
化为极坐标方程, ![]() ,即
,即![]() .
.

【题目】在调查男女乘客是否晕机的情况中,已知男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,![]() 其中
其中 ![]() 为样本容量。
为样本容量。
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)根据以上数据建立一个 ![]() 的列联表;
的列联表;
(2)试判断是否有95%的把握认为是否晕机与性别有关?
【题目】微信已成为人们常用的社交软件,“微信运动”是微信里由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的![]() 或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
步数 性别 | 0 | 2001 | 5001 | 8001 | >10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
若某人一天的走路步数超过8000步被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)利用样本估计总体的思想,试估计小明的所有微信好友中每日走路步数超过10000步的概率;
(2)根据题意完成下面的![]() 列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附: 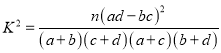
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |