题目内容
10.若定义在区间D上的函数f(x)对于D上的n个值x1,x2,…xn,总满足$\frac{1}{n}[{f({x_1})+f({x_2})+…+f({x_n})}]≤f(\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$),称函数f(x)为D上的凸函数;现已知f(x)=sinx在(0,π)上是凸函数,则△ABC中,sinA+sinB+sinC最大值是$\frac{3\sqrt{3}}{2}$.分析 根据f(x)=sinx在(0,π)上是凸函数以及凸函数的定义可得$\frac{f(A)+f(B)+f(C)}{3}$≤f($\frac{A+B+C}{3}$)=f( $\frac{π}{3}$),即sinA+sinB+sinC≤3sin $\frac{π}{3}$,由此求得sinA+sinB+sinC的最大值.
解答 解::∵f(x)=sinx在区间(0,π)上是凸函数,
且A、B、C∈(0,π),
∴$\frac{f(A)+f(B)+f(C)}{3}$≤f($\frac{A+B+C}{3}$)=f( $\frac{π}{3}$),即sinA+sinB+sinC≤3sin $\frac{π}{3}$=$\frac{3\sqrt{3}}{2}$,
所以sinA+sinB+sinC的最大值为 $\frac{3\sqrt{3}}{2}$.
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题主要考查三角函数的最值问题.关键是利用新定义得到所需内角的三角函数关系;考查了考生运用所给条件分析问题的能力和创造性解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.要得到函数y=sin(2x+$\frac{π}{5}$)的图象,只需将y=sin(x-$\frac{π}{5}$)的图象( )
| A. | 先向右平移$\frac{2π}{5}$个单位,再将横坐标缩小为原来的$\frac{1}{2}$倍 | |
| B. | 先向右平移$\frac{2π}{5}$个单位,再将横坐标扩大为原来的2倍 | |
| C. | 先向左平移$\frac{2π}{5}$个单位,再将横坐标缩小为原来的$\frac{1}{2}$倍 | |
| D. | 先向左平移$\frac{2π}{5}$个单位,再将横坐标扩大为原来的2倍 |
2.已知sinα-sinβ=$\frac{1}{2}$,cosα+cosβ=$\frac{1}{4}$,则cos(α+β)=( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{32}$ | D. | $-\frac{27}{32}$ |
19.已知a=3-2,b=0.3-2,c=log0.32,根据右边程序框图,输出的数是( )
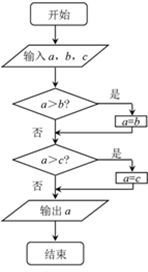

| A. | 3-2 | B. | 0.3-2 | C. | log0.32 | D. | 无法确定 |