题目内容
5.要得到函数y=sin(2x+$\frac{π}{5}$)的图象,只需将y=sin(x-$\frac{π}{5}$)的图象( )| A. | 先向右平移$\frac{2π}{5}$个单位,再将横坐标缩小为原来的$\frac{1}{2}$倍 | |
| B. | 先向右平移$\frac{2π}{5}$个单位,再将横坐标扩大为原来的2倍 | |
| C. | 先向左平移$\frac{2π}{5}$个单位,再将横坐标缩小为原来的$\frac{1}{2}$倍 | |
| D. | 先向左平移$\frac{2π}{5}$个单位,再将横坐标扩大为原来的2倍 |
分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:将y=sin(x-$\frac{π}{5}$)的图象向左平移$\frac{2π}{5}$个单位,得到y=sin(x+$\frac{π}{5}$)的图象,
将y=sin(x+$\frac{π}{5}$)的图象再将横坐标缩小为原来的$\frac{1}{2}$倍(纵坐标不变)可得到函数y=sin(2x+$\frac{π}{5}$)的图象,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.为了得到函数$y=sin(x-\frac{π}{3})(x∈R)$的图象,只需把函数y=sinx的图象上所有的点( )
| A. | 向右平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{3}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
15.某海滨浴场的海浪高度y (米)是时间t(0≤t≤24)(小时)的函数,记作y=f(t),表是某天各时的浪高数据:
(1)选用一个函数来近似描述这个海滨浴场的海浪高度y (米)与t时间(小时)的函数关系;
(2)依据规定,当海浪高度不少于1米时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的上午8时至晚上20时之间,有多少时间可供冲浪爱好者进行冲浪?
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(2)依据规定,当海浪高度不少于1米时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的上午8时至晚上20时之间,有多少时间可供冲浪爱好者进行冲浪?
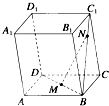 如图,已知ABCD-A1B1C1D1是平行六面体.设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的$\frac{3}{4}$分点,设$\overrightarrow{MN}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$+γ$\overrightarrow{AA1}$,试求α、β、γ的值.
如图,已知ABCD-A1B1C1D1是平行六面体.设M是底面ABCD的中心,N是侧面BCC1B1对角线BC1上的$\frac{3}{4}$分点,设$\overrightarrow{MN}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$+γ$\overrightarrow{AA1}$,试求α、β、γ的值.