题目内容
2.已知sinα-sinβ=$\frac{1}{2}$,cosα+cosβ=$\frac{1}{4}$,则cos(α+β)=( )| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{32}$ | D. | $-\frac{27}{32}$ |
分析 将已知等式两边平方可得:sin2α+sin2β-2sinαsinβ=$\frac{1}{4}$,①,cos${\;}^{2}α+co{s}^{2}β+2cosαcosβ=\frac{1}{16}$,②,①+②利用两角和的余弦函数公式可整理得2+2cos(α+β)=$\frac{5}{16}$,从而得解.
解答 解:∵sinα-sinβ=$\frac{1}{2}$,cosα+cosβ=$\frac{1}{4}$,
∴两边平方可得:sin2α+sin2β-2sinαsinβ=$\frac{1}{4}$,①
cos${\;}^{2}α+co{s}^{2}β+2cosαcosβ=\frac{1}{16}$,②
∴①+②可解得:2+2(cosαcosβ-sinαsinβ)=$\frac{5}{16}$,整理可得:2+2cos(α+β)=$\frac{5}{16}$,
∴解得:cos(α+β)=$-\frac{27}{32}$.
故选:D.
点评 本题主要考查了同角三角函数关系式,两角和的余弦函数公式的应用,属于基础题.

练习册系列答案
相关题目
17.为了得到函数$y=sin(x-\frac{π}{3})(x∈R)$的图象,只需把函数y=sinx的图象上所有的点( )
| A. | 向右平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{3}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
11.下列式子中,错误的是( )
| A. | $(\frac{1}{x})'=-\frac{1}{x^2}$ | B. | (x2cosx+2)′=-x2sinx+2xcosx | ||
| C. | $(\frac{e^x}{x})'=\frac{{{e^x}x+{e^x}}}{x^2}$ | D. | $(x{log_a}x)'={log_a}x+\frac{1}{lna}$ |
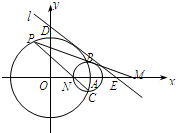 在平面直角坐标系中,圆O:x2+y2=4与x轴的正半轴交于点A,以A为圆心的圆A:(x-2)2+y2=r2(r>0)与圆O交于B,C两点.
在平面直角坐标系中,圆O:x2+y2=4与x轴的正半轴交于点A,以A为圆心的圆A:(x-2)2+y2=r2(r>0)与圆O交于B,C两点.