题目内容

求与x轴相切，圆心在直线3x-y=0上，且被直线x-y=0截得的弦长为2的圆的方程．
由圆心在直线3x-y=0上，设圆心为C（a，3a），
∵圆C与x轴相切，∴点C到x轴的距离等于半径，可得r=|3a|，
由此得到圆的方程为（x-a）2+（y-3）2=9a2，
点C到直线x-y=0的距离为d=
|a-3a|
2
=
2
|a|，
∵圆C被直线x-y=0截得的弦长为2，
∴根据垂径定理，得2
r2-d2
=2，即2
9a2-2a2
=2，解之得a=±
7
7
．
由此可得圆心为C（
7
7
，
3
7
7
）或C（-
7
7
，-
3
7
7
），半径r=
3
7
7

因此，所求的圆的方程是（x-
7
7
）2+（y-
3
7
7
）2=
9
7
或（x+1）2+（y+
3
7
7
）2=
9
7
．
练习册系列答案
相关题目
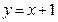已知P是直线上一点，M，N分别是圆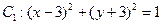与圆上的点则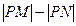的最大值为（    ）
A．4B．3C．2D．1
已知椭圆2x2+y2=2的两焦点为F1，F2，且B为短轴的一个端点，则△F1BF2的外接圆方程为（　　）
A．（x-1）2+y2=4B．x2+y2=1C．x2+y2=4D．x2+（y-1）2=4
若圆x2+y2+Dx+Ey+F=0关于直线l1：x-y+4=0和直线l2；x+3y=0都对称，则D+E的值为（　　）
A．-4B．-2C．2D．4
若圆C以抛物线y2=4x的焦点为圆心，且与抛物线的准线相切，则该圆的标准方程是______．
与圆x2+y2-6x+2y+6=0同圆心且经过点（1，-1）的圆的方程是（　　）
A．（x-3）2+（y+1）2=8B．（x+3）2+（y+1）2=8
C．（x-3）2+（y+1）2=4D．（x+3）2+（y+1）2=4
圆（x-1）2+（y+3）2=2的圆心和半径分别为（　　）
A．（-1，3），2B．（1，-3），
2
C．（1，-3），2D．（-1，3），
2
过点A（1，3）作圆
x=2+cosθ
y=1+sinθ
（θ为参数）的切线，则切线方程是（　　）
A．3x+4y-15=0B．4x+3y-13=0
C．3x+4y-15=0或y=3D．3x+4y-15=0或x=1
若直线y=x+b与函数y=
4-x2
的图有两个不同的交点，则b的取值范围为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网