题目内容
与圆x2+y2-6x+2y+6=0同圆心且经过点（1，-1）的圆的方程是（ ）
| A．（x-3）2+（y+1）2=8 | B．（x+3）2+（y+1）2=8 |
| C．（x-3）2+（y+1）2=4 | D．（x+3）2+（y+1）2=4 |
将圆x2+y2-6x+2y+6=0化成标准方程，得（x-3）2+（y+1）2=4，
∴圆心为C（3，-1），半径为2．
根据所求的圆与圆x2+y2-6x+2y+6=0圆心相同，设其方程为（x-3）2+（y+1）2=r2，
将点（1，-1）代入，得（1-3）2+（-1+1）2=r2，解得r2=4．
∴所求圆的方程为（x-3）2+（y+1）2=4．
∴圆心为C（3，-1），半径为2．
根据所求的圆与圆x2+y2-6x+2y+6=0圆心相同，设其方程为（x-3）2+（y+1）2=r2，
将点（1，-1）代入，得（1-3）2+（-1+1）2=r2，解得r2=4．
∴所求圆的方程为（x-3）2+（y+1）2=4．
练习册系列答案
名校通行证有效作业系列答案
相关题目
,
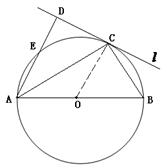
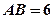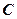为圆周上一点，
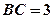,过
，过A作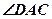
的度数与线段AE的长。