题目内容
若圆x2+y2+Dx+Ey+F=0关于直线l1:x-y+4=0和直线l2;x+3y=0都对称,则D+E的值为( )
| A.-4 | B.-2 | C.2 | D.4 |
将圆x2+y2+Dx+Ey+F=0化成标准方程,得(x+
)2+(y+
)2=
(D2+E2-4F)
∴圆心为C(-
,-
),半径r=
.
又∵直线l1和直线l2都是圆的对称轴,
∴直线l1与直线l2都经过圆的圆心C,它们的交点即为点C.
联解
,可得
,
即圆心为C(-3,1).
因此-
=-3且-
=1,
解得D=6、E=-2,可得D+E=4.
故选:D
| D |
| 2 |
| E |
| 2 |
| 1 |
| 4 |
∴圆心为C(-
| D |
| 2 |
| E |
| 2 |
| 1 |
| 2 |
| D2+E2-4F |
又∵直线l1和直线l2都是圆的对称轴,
∴直线l1与直线l2都经过圆的圆心C,它们的交点即为点C.
联解
|
|
即圆心为C(-3,1).
因此-
| D |
| 2 |
| E |
| 2 |
解得D=6、E=-2,可得D+E=4.
故选:D

练习册系列答案
相关题目
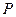 是直线
是直线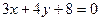 上的动点,
上的动点, 是圆
是圆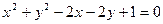 的切线,
的切线,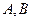 是切点,
是切点,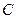 是圆心,那么四边形
是圆心,那么四边形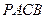 面积的最小值是________________。
面积的最小值是________________。