题目内容
若直线y=x+b与函数y=
的图有两个不同的交点,则b的取值范围为______.
| 4-x2 |
因为y=
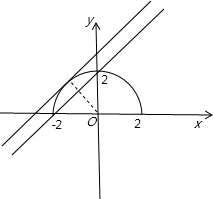
表示圆心坐标为(0,0),半径为2的半圆,
则把直线y=x+b与半圆y=
的图象画出,如图所示,
当直线y=x+b与半圆相切时,
圆心到直线的距离d=
=2,解得b=2
,b=-2
(舍去),
当直线过(0,2)时,直线与半圆有两个交点,
把(0,2)代入直线y=x+b中,解得b=2,
则满足题意的b的范围为:[2,2
).
故答案为:[2,2
)
| 4-x2 |
则把直线y=x+b与半圆y=
| 4-x2 |
当直线y=x+b与半圆相切时,
圆心到直线的距离d=
| |b| | ||
|
| 2 |
| 2 |
当直线过(0,2)时,直线与半圆有两个交点,
把(0,2)代入直线y=x+b中,解得b=2,
则满足题意的b的范围为:[2,2
| 2 |
故答案为:[2,2
| 2 |


练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目