题目内容
【题目】设椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若椭圆C的离心率为
两点,若椭圆C的离心率为![]() ,
,![]() 的周长为8.
的周长为8.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,是否存在实数k使得以
两点,是否存在实数k使得以![]() 为直径的圆恰好经过坐标原点?若存在,求出k的值;若不存在,请说明理由.
为直径的圆恰好经过坐标原点?若存在,求出k的值;若不存在,请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)存在,
(Ⅱ)存在,![]()
【解析】
(I)根据椭圆离心率、椭圆的定义列方程组,解方程组求得![]() 的值,进而求得椭圆的标准方程.
的值,进而求得椭圆的标准方程.
(II)设出![]() 两点的坐标,联立直线
两点的坐标,联立直线![]() 的方程和椭圆方程,计算判别式求得
的方程和椭圆方程,计算判别式求得![]() 的取值范围,并写出根与系数关系,根据圆的几何性质得到
的取值范围,并写出根与系数关系,根据圆的几何性质得到![]() ,由此得到
,由此得到![]() ,由此列方程,解方程求得
,由此列方程,解方程求得![]() 的值.
的值.
(I)由题意知 ,所以所求椭圆的标准方程是
,所以所求椭圆的标准方程是![]() .
.
(II)假设存在这样的实数![]() 使得以
使得以![]() 为直径的圆恰好经过原点.
为直径的圆恰好经过原点.
设![]() ,联立方程组
,联立方程组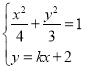 ,
,
消去![]() 得
得![]() ,
,
由题意知,![]() 是此方程的两个实数解,
是此方程的两个实数解,
所以![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() .
.
又因为以![]() 为直径的圆过原点,所以
为直径的圆过原点,所以![]() ,所以
,所以![]() ,
,
而![]() ,
, ![]() ,即
,即![]() ,解得
,解得![]() .
.
故存在这样的直线使得以![]() 为直径的圆过原点.
为直径的圆过原点.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】在一次“综艺类和体育类节目,哪一类节目受中学生欢迎”的调查中,随机调查了男女各100名学生,其中女同学中有73人更爱看综艺类节目,另外27人更爱看体育类节目;男同学中有42人更爱看综艺类节目,另外58人更爱看体育类节目.
(1)根据以上数据填写如下![]() 列联表:
列联表:
综艺类 | 体育类 | 总计 | |
女 | |||
男 | |||
总计 |
(2)试判断是否有![]() 的把握认为“中学生更爱看综艺类节目还是体育类节目与性别有关”.
的把握认为“中学生更爱看综艺类节目还是体育类节目与性别有关”.
参考公式:![]() ,其中
,其中![]() .
.
临界值表:
| 0.025 | 0.01 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成A,B两组,每组20人,A组群众给第一阶段的创文工作评分,B组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图茎叶图:

![]() 根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度![]() 不要求计算出具体值,给出结论即可
不要求计算出具体值,给出结论即可![]() ;
;
![]() 根据群众的评分将满意度从低到高分为三个等级:
根据群众的评分将满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
![]() 由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
![]() 完成下面的列联表,并根据列联表判断是否有
完成下面的列联表,并根据列联表判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | |
第一阶段 | ||
第二阶段 |
附:![]()
|
|
|
|
k |
|
|
|