题目内容
【题目】设λ是正实数，（1+λx）20的二项展开式为a0+a1x+a2x2+…+a20x20，其中a0，a1，…，a20 ，…，均为常数
（1）若a3＝12a2，求λ的值；
（2）若a5≥an对一切n∈{0，1，…，20}均成立，求λ的取值范围．
【答案】（1）λ＝2 （2）
【解析】
（1）根据通项公式可得C
λ3＝12C
λ2，解得λ＝2即可；
（2）假设第r+1项系数最大，根据题意列式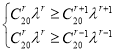
，化简得
，再根据a5≥an对一切n∈{0，1，…，20}均成立，得到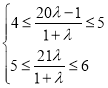
，解不等式组即可得到答案.
（1）通项公式为Tr+1＝
，r＝0，1，2，…，20，
∴由a3＝12a2得，Cλ3＝12Cλ2，解得λ＝2．
（2）假设第r+1项系数最大，因为λ是正实数，依题意得，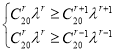
解得
，变形得，
因为a5≥an对一切n∈{0，1，…，20}均成立，
∴∴
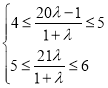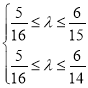，解得
．
【题目】某地因受天气，春季禁渔等因素影响，政府规定每年的7月1日以后的100天为当年的捕鱼期.某渔业捕捞队对吨位为
的20艘捕鱼船一天的捕鱼量进行了统计，如下表所示：
捕鱼量(单位：吨) |
|
|
|
|
|
频数 | 2 | 7 | 7 | 3 | 1 |
根据气象局统计近20年此地每年100天的捕鱼期内的晴好天气情况如下表（捕鱼期内的每个晴好天气渔船方可捕鱼，非晴好天气不捕鱼）：
晴好天气(单位：天) |
|
|
|
|
|
频数 | 2 | 7 | 6 | 3 | 2 |
（同组数据以这组数据的中间值作代表）
（Ⅰ）估计渔业捕捞队吨位为的渔船单次出海的捕鱼量的平均数
；
（Ⅱ）已知当地鱼价为2万元/吨，此种捕鱼船在捕鱼期内捕鱼时，每天成本为10万元/艘，若不捕鱼，每天成本为2万元/艘，若以（Ⅰ）中确定的作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
①请依据往年天气统计数据，试估计一艘此种捕鱼船年利润不少于1600万元的概率；
②设今后3年中，此种捕鱼船每年捕鱼情况一样，记一艘此种捕鱼船年利润不少于1600万元的年数为
，求的分布列和期望.
