题目内容
【题目】已知双曲线C：
与双曲线
有相同的渐近线，且双曲线C过点
．
(1)若双曲线C的左、右焦点分别为
，
，双曲线C上有一点P，使得
，求△
的面积；
(2)过双曲线C的右焦点作直线l与双曲线右支交于A，B两点，若△
的周长是
，求直线l的方程．
【答案】（1）
；（2）
或
.
【解析】
(1)先求出双曲线方程，然后利用双曲线的定义以及余弦定理可求得△
的面积；
(2)通过△
的周长是
以及双曲线的定义可得
，设AB：
，联立：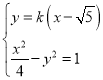
，利用韦达定理以及弦长公式可得
的值，进而可得直线l的方程.
解：(1) 设双曲线C：
，点
代入得：
∴双曲线C：
在△PF1F2中，设
，
∴
，
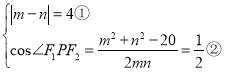由②得：
，
，
，
∴
；
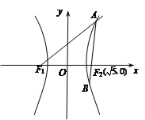
(2) ∵
∴，
1°当直线AB斜率不存在时，
，不符合题意（舍）
2°当直线AB斜率存在时，设AB：，
联立：，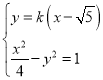
∴
，
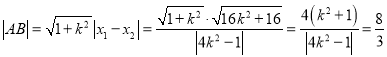解得：
，此时
，
∴直线l方程：
或
.
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
【题目】某地因受天气，春季禁渔等因素影响，政府规定每年的7月1日以后的100天为当年的捕鱼期.某渔业捕捞队对吨位为
的20艘捕鱼船一天的捕鱼量进行了统计，如下表所示：
捕鱼量(单位：吨) |
|
|
|
|
|
频数 | 2 | 7 | 7 | 3 | 1 |
根据气象局统计近20年此地每年100天的捕鱼期内的晴好天气情况如下表（捕鱼期内的每个晴好天气渔船方可捕鱼，非晴好天气不捕鱼）：
晴好天气(单位：天) |
|
|
|
|
|
频数 | 2 | 7 | 6 | 3 | 2 |
（同组数据以这组数据的中间值作代表）
（Ⅰ）估计渔业捕捞队吨位为的渔船单次出海的捕鱼量的平均数
；
（Ⅱ）已知当地鱼价为2万元/吨，此种捕鱼船在捕鱼期内捕鱼时，每天成本为10万元/艘，若不捕鱼，每天成本为2万元/艘，若以（Ⅰ）中确定的作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
①请依据往年天气统计数据，试估计一艘此种捕鱼船年利润不少于1600万元的概率；
②设今后3年中，此种捕鱼船每年捕鱼情况一样，记一艘此种捕鱼船年利润不少于1600万元的年数为
，求的分布列和期望.
