题目内容
19.在平面直角坐标系xOy中,已知椭圆C的中心在原点O,焦点在x轴上,短轴长为2,离心率为$\frac{\sqrt{2}}{2}$,过左顶点A的直线l与椭圆交于另一点B.(Ⅰ)求椭圆C的方程;
(Ⅱ)若|AB|=$\frac{4}{3}$,求直线l的倾斜角.
分析 (Ⅰ)根据题目条件可列式求得椭圆方程.
(Ⅱ)设直线l的方程为:y=k(x+$\sqrt{2}$),代入椭圆方程,由弦长公式得到所需结论.
解答 解:(Ⅰ)由题意得:$\left\{\begin{array}{l}{2b=2}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$则$\left\{\begin{array}{l}{b=1}\\{a=\sqrt{2}}\end{array}\right.$得椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$
(Ⅱ)由题意直线得斜率存在,因为左顶点为(-$\sqrt{2},0$)
设直线l的方程为:y=k(x+$\sqrt{2}$)
代入椭圆方程得:$(2{k}^{2}+1){x}^{2}+4\sqrt{2}{k}^{2}x+4{k}^{2}-2=0$
因为一根为${x}_{1}=-\sqrt{2}$,则另一根为${x}_{2}=\frac{\sqrt{2}-2\sqrt{2}{k}^{2}}{2{k}^{2}+1}$
则AB|=$\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|=\sqrt{1+{k}^{2}}$$\frac{2\sqrt{2}}{2{k}^{2}+1}=\frac{4}{3}$
化简得8k2-k-7=0,即k2=1,k=±1,则倾斜角为45°或135°.
点评 本题主要考查了圆锥曲线方程的求法和圆锥曲线与直线的综合应用,属于中档题,在高考中时常涉及.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).
如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).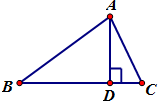 如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )
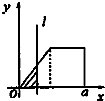
如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )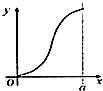 如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )
如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )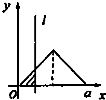
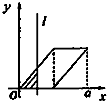
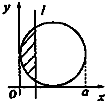
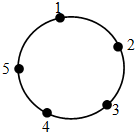 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.