题目内容
11.已知函数$f(x)=ln(x+a)+\frac{2}{x}$,g(x)=lnx.(注:${[{ln(x+a)}]^′}=\frac{1}{x+a}$)(1)a=0时,求函数f(x)的单调区间和极值;
(2)已知f(x)在[e,+∞)上是单调函数,求a的取值范围;
(3)已知m,n,ξ满足n>ξ>m>0,且$g'(ξ)=\frac{g(n)-g(m)}{n-m}$,试比较ξ与$\sqrt{mn}$的大小.
分析 (1)对f(x)求导,利用导数求得f(x)的单调区间
(2)对f(x)求导,分离参数a,利用导数的性质求得a的取值范围
(3)构造新函数,利用新函数的导数证明命题成立.
解答 解:(1)a=0,f(x)=lnx+$\frac{2}{x}$,f'(x)=$\frac{1}{x}-\frac{2}{{x}^{2}}=\frac{x-2}{{x}^{2}}$,f'(x)=0,x=2.
∵x>0,∴f(x)的单调增区间为(2,+∞),减区间为(0,2).且x=2时f(x)取得极小值f(2)=ln2+1
(2)∵$f(x)=ln({x+a})+\frac{2}{x}$∴$f'(x)=\frac{1}{x+a}-\frac{2}{x^2}=\frac{{{x^2}-2x-2a}}{{{x^2}({x+a})}}$,∵f(x)在[e,+∞)上单调∴$\left\{\begin{array}{l}x+a>0\\{x^2}-2x-2a≥0\end{array}\right.$或$\left\{\begin{array}{l}x+a>0\\{x^2}-2x-2a≤0\end{array}\right.$∴$\left\{\begin{array}{l}a>-e\\ a≤\frac{1}{2}{x^2}-x\end{array}\right.$或$\left\{\begin{array}{l}a>-e\\ a≥\frac{1}{2}{x^2}-x\end{array}\right.$∵当x≥e时,$\frac{1}{2}{x^2}-x≥\frac{1}{2}{e^2}-e$
∴$-e<a≤\frac{1}{2}{e^2}-e$…8分
(2)∵$g'(ξ)=\frac{g(n)-g(m)}{n-m}$∴$\frac{1}{ξ}=\frac{lnn-lnm}{n-m}$
设$h(x)=2lnx-x+\frac{1}{x}({x>1})$,则$h'(x)=\frac{2}{x}-1-\frac{1}{x^2}=-\frac{{{{({x-1})}^2}}}{x^2}<0$
∴h(x)<h(1)=0,∴当x>1时,$2lnx<x-\frac{1}{x}$
令$x=\sqrt{\frac{n}{m}}$,得$2ln\sqrt{\frac{n}{m}}<\sqrt{\frac{n}{m}}-\sqrt{\frac{m}{n}}$∴$lnn-lnm<\frac{n-m}{{\sqrt{mn}}}$⇒$\frac{lnn-lnm}{n-m}<\frac{1}{{\sqrt{mn}}}$∴$\frac{1}{ξ}<\frac{1}{{\sqrt{mn}}}$即$ξ>\sqrt{mn}$…14分.
点评 本题主要考查导数在求得参数的取值范围的应用,属于中档题,在高考中常作压轴题出现.

| A. | [1,+∞) | B. | (0,1] | C. | [3,+∞) | D. | [1,3] |
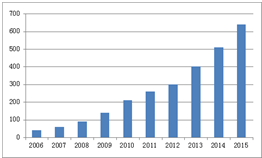 某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )
某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=ax3+b | D. | y=alnx+b |