题目内容
7.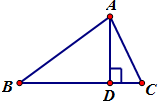 如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )
如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 通过向量的运算法则及三角函数的定义可得$\overrightarrow{AD}$•$\overrightarrow{AC}$=4sin2θ,利用θ∈[$\frac{π}{6}$,$\frac{π}{3}$],计算即得结论.
解答 解:易知$\overrightarrow{AD}$•$\overrightarrow{AC}$=$\overrightarrow{AD}$•($\overrightarrow{BC}$-$\overrightarrow{BA}$)=$\overrightarrow{AD}$•$\overrightarrow{BC}$-$\overrightarrow{AD}$•$\overrightarrow{BA}$,
∵AD是边BC上的高,∴$\overrightarrow{AD}$•$\overrightarrow{BC}$=0,
∴$\overrightarrow{AD}$•$\overrightarrow{AC}$=-$\overrightarrow{AD}$•$\overrightarrow{BA}$=$\overrightarrow{AD}$•$\overrightarrow{AB}$,
又∵AB=2,∠ABC=θ,△ABD为直角三角形,
∴AD=ABsinθ=2sinθ,
∴$\overrightarrow{AD}$•$\overrightarrow{AB}$=$2sinθ×2×cos(\frac{π}{2}-θ)$
=4sinθ•sinθ
=4sin2θ,
∵θ∈[$\frac{π}{6}$,$\frac{π}{3}$],∴sinθ∈[$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$],
∴4sin2θ∈[1,3],即$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值分别为3与1,
故选:B.
点评 本题以三角形为载体,考查平面向量数量积的运算,注意解题方法的积累,属于中档题.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
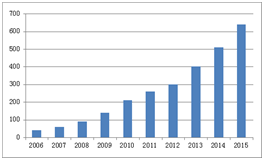 某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )
某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=ax3+b | D. | y=alnx+b |
| 时间x/小时 | 2 | 3 | 5 | 8 | 9 | 12 |
| 工资y/元 | 30 | 40 | 60 | 90 | 120 | m |
| A. | 125元 | B. | 128元 | C. | 140元 | D. | 142.7元 |