题目内容
9. 如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).
如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).(1)若P为BD的中点,求证:AP⊥BC;
(2)若二面角B-PC-A的余弦值为$\frac{2\sqrt{19}}{19}$,求直线PN与平面ABD所成角的正弦值.
分析 (1)取BC的中点E,连结AE、AM、MC,利用中位线定理及线面平面的判定定理即得结论;
(2)以C为原点,建立空间直角坐标系,通过点p是BD上的动点,可得t$\overrightarrow{BD}$=$\overrightarrow{BP}$,则P(1-t,$\sqrt{3}$-$\sqrt{3}$t,4t),0<t<1,
利用图形判断$\overrightarrow{AE}$=($-\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,0)为面BCP的向量,面ACP的法向量为$\overrightarrow{{n}_{1}}$=(0,4,$\frac{\sqrt{3}t-\sqrt{3}}{t}$),根据|cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{AE}$>|=|$\frac{2\sqrt{3}}{\sqrt{3}×(\frac{\sqrt{3}t-\sqrt{3}}{t})^{2}}$|=$\frac{2\sqrt{19}}{19}$,
求解t=$\frac{1}{2}$,确定$\overrightarrow{NP}$=(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,0),p($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,2),面ABD的法向量为;$\overrightarrow{{n}_{2}}$=($\sqrt{3}$,1,$\frac{\sqrt{3}}{2}$),利用向量的数量积sinα=|cos<$\overrightarrow{{n}_{2}}$,$\overrightarrow{NP}$>|求解即可.
解答 证明:(1)(1)证明:取BC的中点E,连结AE、AP、PC,
∵CD⊥平面ABC,DC∥AN,
∴AN⊥平面ABC,∴AN⊥BC,
又∵P为BD的中点,
∴PE∥CD∥AN,即PE⊥BC,
∵AB=AC=BC,E为BC中点,
∴AE⊥BC,
∴BC⊥平面AEP,
∴AP⊥BC;
(II)解:以C为原点,建立空间直角坐标系如图,
∵CD=2AN=4,又AB=AC=BC=2,
∴C(0,0,0),A(2,0,0),B(1,$\sqrt{3}$,0),
D(0,0,4),N(2,0,2),
则$\overrightarrow{CB}$=(1,$\sqrt{3}$,0),$\overrightarrow{CA}$=(2,0,0),$\overrightarrow{BD}$=(-1,-$\sqrt{3}$,4),
设t$\overrightarrow{BD}$=$\overrightarrow{BP}$,则P(1-t,$\sqrt{3}$-$\sqrt{3}$t,4t),0<t<1
∴$\overrightarrow{NP}$=(-1-t,$\sqrt{3}$-$\sqrt{3}$t,4t-2),$\overrightarrow{CP}$=(1-t,$\sqrt{3}$-$\sqrt{3}$t,4t)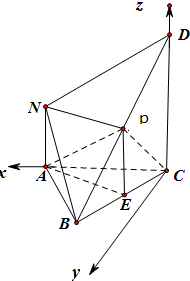
B,D中点为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,2),在面ABC的射影E($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,0),$\overrightarrow{AE}$=($-\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,0)为面BCP的向量,
面ACP的法向量为;$\overrightarrow{{n}_{1}}$=(x1,y1,z1),
$\left\{\begin{array}{l}{2{x}_{1}=0}\\{(1-t){x}_{1}+(\sqrt{3}-\sqrt{3}t){y}_{{\;}_{1}}+4t{z}_{1}=0}\end{array}\right.$得出$\overrightarrow{{n}_{1}}$=(0,4,$\frac{\sqrt{3}t-\sqrt{3}}{t}$),
∵|cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{AE}$>|=|$\frac{2\sqrt{3}}{\sqrt{3}×(\frac{\sqrt{3}t-\sqrt{3}}{t})^{2}}$|=$\frac{2\sqrt{19}}{19}$,t=$\frac{1}{2}$,
∴$\overrightarrow{NP}$=(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,0),p($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,2),
设面ABD的法向量为;$\overrightarrow{{n}_{2}}$=(x2,y2,z2),$\overrightarrow{AB}$=(-1,$\sqrt{3}$,0),$\overrightarrow{BD}$=(-1,-$\sqrt{3}$,4),
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{BD}=0}\end{array}\right.$即$\left\{\begin{array}{l}{-{x}_{2}+\sqrt{3}{y}_{2}=0}\\{-{x}_{2}-\sqrt{3}{y}_{2}+4{z}_{2}=0}\end{array}\right.$得出$\overrightarrow{{n}_{2}}$=($\sqrt{3}$,1,$\frac{\sqrt{3}}{2}$),$\overrightarrow{NP}$$•\overrightarrow{{n}_{2}}$=-$\sqrt{3}$,|$\overrightarrow{{n}_{2}}$|=$\frac{\sqrt{19}}{2}$,|$\overrightarrow{NP}$|=$\sqrt{3}$,
∵cos<$\overrightarrow{{n}_{2}}$,$\overrightarrow{NP}$>=$\frac{-\sqrt{3}}{\sqrt{3}×\frac{\sqrt{19}}{2}}$=$-\frac{2\sqrt{19}}{19}$
∴直线PN与平面ABD所成角的正弦值:sinα=|cos<$\overrightarrow{{n}_{2}}$,$\overrightarrow{NP}$>|=$\frac{2\sqrt{19}}{19}$
点评 本题考查线面垂直的判定定理,二面角的计算,数量积的运算,平方关系,注意解题方法的积累,属于难题,多次力平面的法向量求解问题,准确计算是解题的关键.

| A. | [1,+∞) | B. | (0,1] | C. | [3,+∞) | D. | [1,3] |
 如图所示,圆锥顶点为P,底面圆心为O,AB和CD是底面圆O上的两条平行弦,证明:平面PAD与平面PCD的交线平行于底面.
如图所示,圆锥顶点为P,底面圆心为O,AB和CD是底面圆O上的两条平行弦,证明:平面PAD与平面PCD的交线平行于底面.