如图.一只青蛙在圆周上标有数字的五个点上跳.若它停在奇数点上.则下一次沿顺时针方向跳两个点.若它停在偶数点上.则下一次沿逆时针方向跳一个点.若青蛙从5这个点开始跳.则经2015次跳后停在的点对应的数为3．题目和参考答案——青夏教育精英家教网—

题目内容

8．

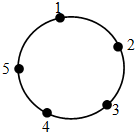如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下一次沿顺时针方向跳两个点，若它停在偶数点上，则下一次沿逆时针方向跳一个点，若青蛙从5这个点开始跳，则经2015次跳后停在的点对应的数为3．

分析根据题意，分析可得青蛙的跳动规律为2-1-3-5，周期为4；又由2015=4×503+3，经过2015次跳后它停在的点所对应的数为3．

解答解：由5起跳，5是奇数，沿顺时针下一次能跳2个点，落在2上．
由2起跳，2是偶数，沿逆时针下一次只能跳一个点，落在1上
1是奇数，沿顺时针跳两个点，落在3上．
由3起跳，是奇偶数，沿顺时针跳两个点，落在5上．
2-1-3-5-2，周期为4；又由2015=4×503+3，
∴经过2015次跳后它停在的点所对应的数为3．
故答案为：3．

点评此题主要考查了数的变化规律，得到青蛙落在数字上的循环规律是解决本题的关键．

练习册系列答案

19．在平面直角坐标系xOy中，已知椭圆C的中心在原点O，焦点在x轴上，短轴长为2，离心率为$\frac{\sqrt{2}}{2}$，过左顶点A的直线l与椭圆交于另一点B．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若|AB|=$\frac{4}{3}$，求直线l的倾斜角．

16．已知函数$f（x）=\left\{\begin{array}{l}-{x^2}\;，\;x≥0\\{x^2}+2x，\;x＜0\end{array}\right.$，则f（2）=-4；不等式f（x）＜3的解{x|x＞-3}．

3．已知函数f（x）=$\left\{\begin{array}{l}-{x^2}\;，\;x≥0\\{x^2}+2x，\;x＜0\end{array}$，则f（f（-2））=0；不等式f（f（x））≤3的解集为（-∞，$\sqrt{3}$]．

13．

如图是一个有底的容器的三视图，现向容器中匀速注水，容器中水面的高度随时间变化的可能图象是（　　）

20．已知⊙C的极坐标方程为：ρ²-4$\sqrt{2}ρsin（θ+\frac{π}{4}）+6=0$
（Ⅰ）求圆C在直角坐标系中的圆心坐标，并选择合适的参数，写出圆C的参数方程；
（Ⅱ）点P（x，y）在圆C上，试求u=xy的值域．

17．一台仪器每启动一次都随机地出现一个5位的二进制数$A=\overline{{a_1}{a_2}{a_3}{a_4}{a_5}}$，其中A的各位数字中a₁=1，a_k（k=2，3，4，5）出现0的概率为$\frac{1}{3}$，a_k（k=2，3，4，5）出现1的概率为$\frac{2}{3}$，记X=a₁+a₂+a₃+a₄+a₅．当启动仪器一次时，
（Ⅰ）求X=3的概率；
（Ⅱ）求随机变量X的分布列及X的数学期望，并指出当X为何值时，其概率最大．

18．定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$，函数$f（x）=|{\begin{array}{l}{2sinx}&m\\{cos2x}&{cosx}\end{array}}|$的图象关于直线x=$\frac{π}{8}$对称，则f（x）的单调递增区间为（　　）

	A．	$[kπ-\frac{3π}{8}，kπ+\frac{π}{8}]，（k∈Z）$		B．	$[kπ-\frac{π}{8}，kπ+\frac{3π}{8}]，（k∈Z）$
	C．	$[2kπ-\frac{3π}{4}，2kπ+\frac{π}{4}]，（k∈Z）$		D．	$[2kπ-\frac{π}{4}，2kπ+\frac{3π}{4}]，（k∈Z）$

试题分类