题目内容
14．
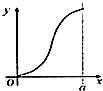如图，有四个平面图形分别是三角形、平行四边形、直角梯形、圆．垂直于x轴的直线l：x=t（0≤t≤a）经过原点O向右平行移动，l在移动过程中扫过平面图形的面积为y（图中阴影部分），若函数y=f（t）的大致图象如图，那么平面图形的形状不可能是（ ）| A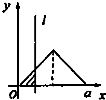． |  | B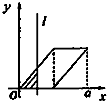． |  | C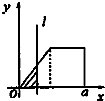． |  | D． |  |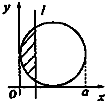
分析 直接利用图形的形状，结合图象，判断不满足的图形即可．
解答 解：由函数的图象可知，几何体具有对称性，
选项A、B、D，l在移动过程中扫过平面图形的面积为y，在中线位置前，都是先慢后快，然后相反．
选项C，后面是直线增加，不满足题意；
故选：C、
点评 本题考查函数的图象与图形面积的变换关系，考查分析问题解决问题的能力．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
2．
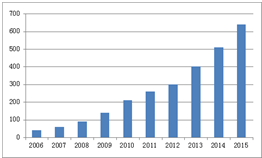某电影院统计电影放映场次的情况如图所示．下列函数模型中，最不合适近似描述电影放映场次逐年变化规律的是（ ）
某电影院统计电影放映场次的情况如图所示．下列函数模型中，最不合适近似描述电影放映场次逐年变化规律的是（ ）| A． | y=ax2+bx+c | B． | y=aex+b | C． | y=ax3+b | D． | y=alnx+b |
9．函数f（x）=x3-ax2-bx+a2在x=1处有极值10，则a，b的值为（ ）
| A． | $\left\{\begin{array}{l}{a=3}\\{b=-3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$ | D． | 以上都不对 |