题目内容
4.已知数列{an}的前n项和为Sn,且a1=1,点(an+1,Sn)(n∈N*)恒在直线x-y-1=0上,数列{bn}是等差数列,且b3=2,b6=8.(1)求数列{an}的通项公式;
(2)若对?n∈N*,(Sn+1)•k≥bn恒成立,求实数k的取值范围.
分析 (1)通过点(an+1,Sn)(n∈N*)恒在直线x-y-1=0上,可得Sn=an+1-1,利用an+1=Sn+1-Sn,计算即得结论;
(2)设数列{bn}的公差为d,利用d=$\frac{{b}_{6}-{b}_{3}}{3}$,计算可得bn=2n-4,条件等价于“对?n∈N*,k≥$\frac{n-2}{{2}^{n-1}}$恒成立”,通过判断cn=$\frac{n-2}{{2}^{n-1}}$的单调性即得结论.
解答 解:(1)∵点(an+1,Sn)(n∈N*)恒在直线x-y-1=0上,
∴an+1-Sn-1=0,即Sn=an+1-1,Sn+1=an+2-1,
∴an+1=Sn+1-Sn=an+2-an+1,即$\frac{{a}_{n+2}}{{a}_{n+1}}$=2,
又∵a1=1,a2=a1+1=2,
∴数列{an}的通项为:an=2n-1;
(2)设数列{bn}的公差为d,
∵b3=2,b6=8,
∴d=$\frac{{b}_{6}-{b}_{3}}{3}$=$\frac{8-2}{3}$=2,b1=b3-2d=2-2×2=-2,
∴数列{bn}的通项为:bn=-2+2(n-1)=2n-4,
又由(1)知Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1,
∴“对?n∈N*,(Sn+1)•k≥bn恒成立”等价于“对?n∈N*,2n•k≥2n-4恒成立”,
即k≥$\frac{n-2}{{2}^{n-1}}$恒成立,记cn=$\frac{n-2}{{2}^{n-1}}$,
则cn+1-cn=$\frac{n-1}{{2}^{n}}$-$\frac{n-2}{{2}^{n-1}}$=$\frac{-n+3}{{2}^{n}}$,
∴当n≤3时,cn+1≥cn;当n≥4时,cn+1<cn;
∴(cn)max=c4=$\frac{4-2}{{2}^{4-1}}$=$\frac{1}{4}$,
∴实数k的取值范围为:[$\frac{1}{4}$,+∞).
点评 本题考查求数列的通项,考查数列的单调性,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| 时间x/小时 | 2 | 3 | 5 | 8 | 9 | 12 |
| 工资y/元 | 30 | 40 | 60 | 90 | 120 | m |
| A. | 125元 | B. | 128元 | C. | 140元 | D. | 142.7元 |
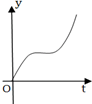
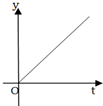
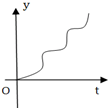
 如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )
如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )