题目内容
已知函数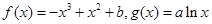 .
.
(1)若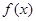 在
在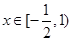 上的最大值为
上的最大值为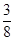 ,求实数
,求实数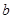 的值;
的值;
(2)若对任意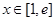 ,都有
,都有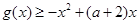 恒成立,求实数
恒成立,求实数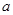 的取值范围;
的取值范围;
(3)在(1)的条件下,设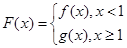 ,对任意给定的正实数
,对任意给定的正实数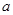 ,曲线
,曲线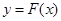 上是否存在两点
上是否存在两点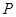 、
、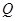 ,使得
,使得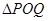 是以
是以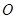 (
(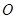 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在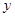 轴上?请说明理由。
轴上?请说明理由。
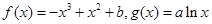 .
.(1)若
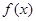 在
在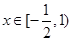 上的最大值为
上的最大值为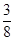 ,求实数
,求实数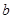 的值;
的值;(2)若对任意
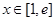 ,都有
,都有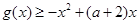 恒成立,求实数
恒成立,求实数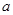 的取值范围;
的取值范围;(3)在(1)的条件下,设
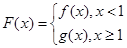 ,对任意给定的正实数
,对任意给定的正实数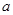 ,曲线
,曲线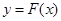 上是否存在两点
上是否存在两点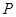 、
、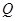 ,使得
,使得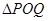 是以
是以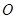 (
(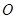 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在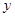 轴上?请说明理由。
轴上?请说明理由。(1)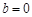 (2)
(2)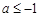 (3)对任意给定的正实数
(3)对任意给定的正实数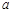 ,曲线
,曲线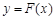 上总存在两点
上总存在两点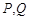 ,使得
,使得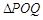 是以
是以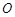 (
(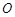 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在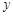 轴上
轴上
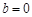 (2)
(2)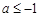 (3)对任意给定的正实数
(3)对任意给定的正实数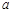 ,曲线
,曲线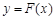 上总存在两点
上总存在两点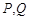 ,使得
,使得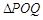 是以
是以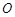 (
(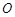 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在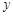 轴上
轴上试题分析:(1)由
 ,得
,得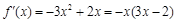 ,
,令
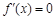 ,得
,得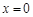 或
或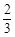 .
.列表如下:
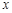 | 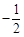 | 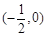 | 0 | 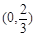 | 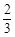 | 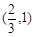 |
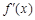 | | 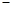 | 0 | 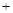 | 0 | 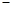 |
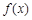 | 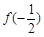 | 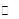 | 极小值 | 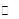 | 极大值 | 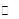 |
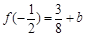 ,
,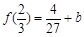 ,
,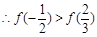 ,
,即最大值为
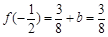 ,
,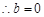 . 4分
. 4分(2)由
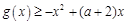 ,得
,得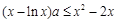 .
.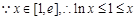 ,且等号不能同时取,
,且等号不能同时取,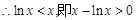 ,
,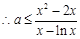 恒成立,即
恒成立,即 .
. 令
 ,求导得,
,求导得,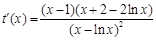 ,
,当
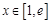 时,
时,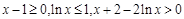 ,从而
,从而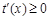 ,
,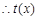 在
在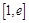 上为增函数,
上为增函数,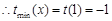 ,
,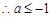 . 8分
. 8分(3)由条件,
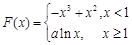 ,
,假设曲线
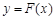 上存在两点
上存在两点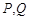 满足题意,则
满足题意,则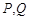 只能在
只能在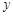 轴两侧,
轴两侧,不妨设
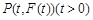 ,则
,则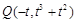 ,且
,且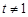 .
.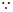
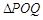 是以
是以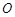 (
( 为坐标原点)为直角顶点的直角三角形,
为坐标原点)为直角顶点的直角三角形,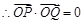 ,
,
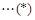 , 10分
, 10分是否存在
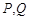 等价于方程
等价于方程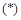 在
在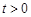 且
且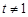 时是否有解.
时是否有解. ①若
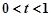 时,方程
时,方程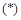 为
为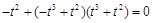 ,化简得
,化简得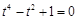 ,
,此方程无解; 11分
②若
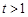 时,
时,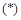 方程为
方程为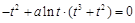 ,即
,即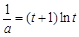 ,
,设
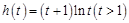 ,则
,则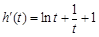 ,
,显然,当
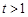 时,
时,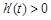 ,即
,即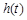 在
在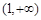 上为增函数,
上为增函数,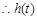 的值域为
的值域为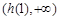 ,即
,即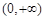 ,
, 当
当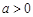 时,方程
时,方程 总有解.
总有解. 对任意给定的正实数
对任意给定的正实数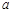 ,曲线
,曲线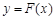 上总存在两点
上总存在两点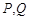 ,使得
,使得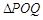 是以
是以 (
(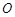 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在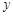 轴上. 14分
轴上. 14分 点评:求函数最值通过函数导数求得极值,比较极值与闭区间的边界值的大小得最值,不等式恒成立中求参数范围的题目常采用分离参数法转化为求函数最值的问题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
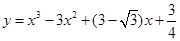 上移动,经过点P的切线的倾斜角为
上移动,经过点P的切线的倾斜角为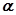 ,则角
,则角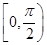
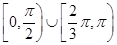
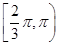
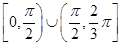
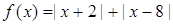 的最小值为
的最小值为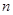 ,则二项式
,则二项式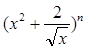 的展开式中的常数项是
的展开式中的常数项是 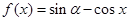 ,则
,则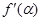 等于( )
等于( )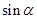
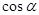
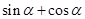
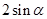
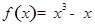 .
.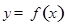 在点
在点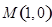 处的切线方程;
处的切线方程;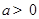 ,如果过点
,如果过点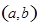 可作曲线
可作曲线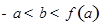
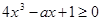 对
对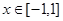 恒成立,则
恒成立,则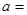 。
。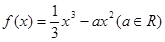 ,若对任意实数
,若对任意实数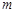 ,直线
,直线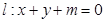 ,都不是曲线
,都不是曲线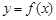 的切线,则实数
的切线,则实数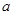 的取值范围是
的取值范围是
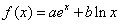 ,且
,且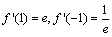 ,则
,则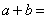 。
。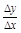 为 .
为 .