题目内容
已知函数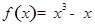 .
.
(1)求曲线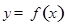 在点
在点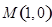 处的切线方程;
处的切线方程;
(2)求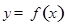 的单调区间.
的单调区间.
(3)设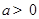 ,如果过点
,如果过点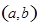 可作曲线
可作曲线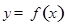 的三条切线,证明:
的三条切线,证明: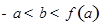
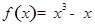 .
.(1)求曲线
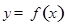 在点
在点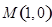 处的切线方程;
处的切线方程;(2)求
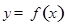 的单调区间.
的单调区间.(3)设
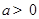 ,如果过点
,如果过点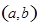 可作曲线
可作曲线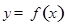 的三条切线,证明:
的三条切线,证明: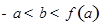
(1)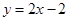
(2)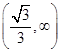 是增区间;
是增区间;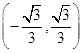 是减区间
是减区间
(3)根据导数的几何意义,结合极值的符号来得到比较大小。
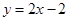
(2)
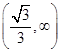 是增区间;
是增区间;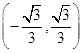 是减区间
是减区间(3)根据导数的几何意义,结合极值的符号来得到比较大小。
试题分析:解:①根据题意,由于函数
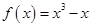 .则可知函数
.则可知函数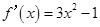 ,那么曲线
,那么曲线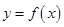 在点
在点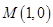 处的切线斜率为2,那么根据点斜式方程可知
处的切线斜率为2,那么根据点斜式方程可知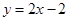
②结合函数的导数的符号得到
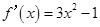 ,那么当导数大于零时,得到x的范围是
,那么当导数大于零时,得到x的范围是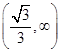 是增区间;当导数小于零时,得到的x的范围是
是增区间;当导数小于零时,得到的x的范围是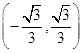 是减区间
是减区间③设切点为
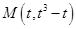 ,
,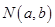
易知
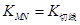 ,所以
,所以 ,
,可化为
 ①
①于是,若过点
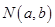 可作曲线
可作曲线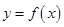 的三条切线,则方程①有三个相异实数根,记
的三条切线,则方程①有三个相异实数根,记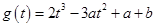 ,
,则
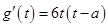 ,易知
,易知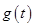 的极大值为
的极大值为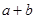 ,极小值为
,极小值为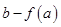
综上,如果过
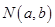 可作曲线三条切线,则
可作曲线三条切线,则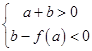
即:
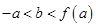
点评:主要是考查了导数在研究函数中的运用,属于基础题。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
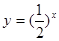 在
在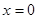 点处的切线方程是( )
点处的切线方程是( )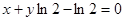
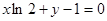
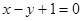
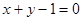
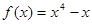 在点P处的切线平行于直线
在点P处的切线平行于直线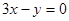 ,则点P的坐标为 ( )
,则点P的坐标为 ( )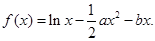 (1)当
(1)当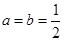 时,求
时,求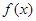 的最大值;(2)令
的最大值;(2)令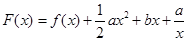 ,(
,(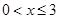 ),其图象上任意一点
),其图象上任意一点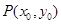 处切线的斜率
处切线的斜率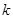 ≤
≤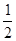 恒成立,求实数
恒成立,求实数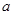 的取值范围;(3)当
的取值范围;(3)当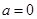 ,
,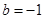 ,方程
,方程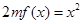 有唯一实数解,求正数
有唯一实数解,求正数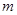 的值.
的值.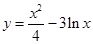 的一条切线的斜率为
的一条切线的斜率为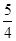 ,则切点的横坐标为( )
,则切点的横坐标为( )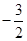
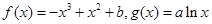 .
.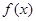 在
在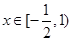 上的最大值为
上的最大值为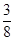 ,求实数
,求实数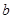 的值;
的值;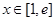 ,都有
,都有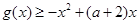 恒成立,求实数
恒成立,求实数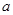 的取值范围;
的取值范围;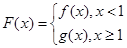 ,对任意给定的正实数
,对任意给定的正实数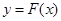 上是否存在两点
上是否存在两点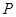 、
、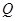 ,使得
,使得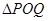 是以
是以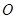 (
(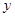 轴上?请说明理由。
轴上?请说明理由。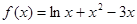 的导函数
的导函数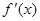 的图象与x轴所围
的图象与x轴所围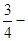 1n2
1n2 1n2
1n2 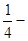 1n2
1n2  1n2
1n2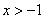 ,试比较
,试比较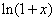 与
与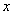 的大小;
的大小;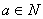 ,使得
,使得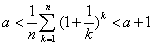 对任意大于
对任意大于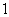 的自然数
的自然数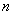 都成立?若存在,试求出
都成立?若存在,试求出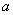 的值并证明你的结论;若不存在,请说明理由。
的值并证明你的结论;若不存在,请说明理由。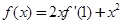 ,则
,则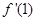 =______________.
=______________.