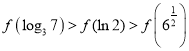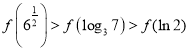题目内容
【题目】目前共享单车基本覆盖饶城市区,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
(1)任选出一名学生,求他(她)骑行过共享单车的概率;
(2)随着单车投放数量增加,乱停乱放成为城市管理的问题,如表是本市某组织累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间关系图表:
之间关系图表:
累计投放单车数量 | 100000 | 120000 | 150000 | 200000 | 230000 |
乱停乱放单车数量 | 1400 | 1700 | 2300 | 3000 | 3600 |
计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() ,
,![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
(3)已知信州区、广丰区、上饶县、经开区四区中,其中有两个区的单车乱停乱放数量超过标准,在“大美上饶”活动中,检查组随机抽取两个区调查单车乱停乱放数量,![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
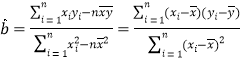 ,
,![]() ,
,
![]() ,
,![]()
【答案】(1)![]() ;(2)
;(2)![]() 162;(3)见解析
162;(3)见解析
【解析】分析:(1)利用古典概型的概率公式求任选一学生骑行过单车的概率.(2)利用最小二乘法原理求回归直线方程,并预测当![]() 时,单车乱停乱放的数量.(3)先写出
时,单车乱停乱放的数量.(3)先写出![]() 的取值为0,1,2,再求每个值的概率,再求其分布列和期望.
的取值为0,1,2,再求每个值的概率,再求其分布列和期望.
详解:(1)骑行单车的学生人数为![]() ,
,
故任选一学生骑行过单车的概率为![]() .
.
(2)由题意得![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
故所求回归方程为![]() ,
,
当![]() 时,
时,![]() ,
,
即单车投放累计26000辆时,乱停乱放的单车数量为162.
(3)![]() 的取值为0,1,2,
的取值为0,1,2,
![]() ;
;![]() ;
;![]() ,
,
![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
![]() .
.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到如表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到如表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(Ⅰ)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(Ⅱ)①现从所抽取的30岁以上的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出3人赠送优惠券,求选出的3人中至少有2人经常使用共享单车的概率.
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用共享单车的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: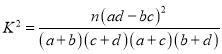 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】为提升教师专业功底,引领青年教师成长,某市教育局举行了全市“园丁杯”课堂教学比赛,在这次比赛中,通过采用录像课评比的片区预赛,有![]() 共10位选手脱颖而出进入全市决赛.决赛采用现场上课形式,从学科评委库中采用随机抽样抽选代号1,2,3,…,7的7名评委,规则是:选手上完课,评委们当初评分,并从7位评委评分中去掉一个最高分,去掉一个最低分,根据剩余5位评委的评分,算出平均分作为该选手的最终得分.记评委
共10位选手脱颖而出进入全市决赛.决赛采用现场上课形式,从学科评委库中采用随机抽样抽选代号1,2,3,…,7的7名评委,规则是:选手上完课,评委们当初评分,并从7位评委评分中去掉一个最高分,去掉一个最低分,根据剩余5位评委的评分,算出平均分作为该选手的最终得分.记评委![]() 对某选手评分排名与该选手最终排名的差的绝对值为“评委
对某选手评分排名与该选手最终排名的差的绝对值为“评委![]() 对这位选手的分数排名偏差”
对这位选手的分数排名偏差”![]() .排名规则:由高到低依次排名,如果选手分数一样,认定名次并列(如:选手
.排名规则:由高到低依次排名,如果选手分数一样,认定名次并列(如:选手![]() 分数一致排在第二,则认为他们同属第二名,没有第三名,接下来分数为第四名).七位评委评分情况如下表所示:
分数一致排在第二,则认为他们同属第二名,没有第三名,接下来分数为第四名).七位评委评分情况如下表所示:
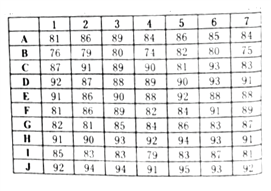
(1)根据最终评分表,填充如下表格:

(2)试借助评委评分分析表,根据评委对各选手的排名偏差的平方和,判断评委4与评委5在这次活动中谁评判更准确.
____号评委评分分析表
选手 | A | B | C | D | E | F | G | H | I | J |
最终排名 | ||||||||||
评分排名 | ||||||||||
排名偏差 |
(3)从这10位选手中任意选出3位,记其中评委4比评委5对选手排名偏差小的选手数位![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.