题目内容
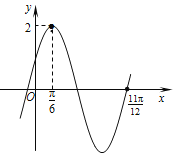
【题目】定义在区间![]() 上的函数
上的函数![]() 的图象如图所示,记为
的图象如图所示,记为![]() ,
,![]() ,
,![]() 为顶点的三角形的面积为
为顶点的三角形的面积为![]() ,则函数
,则函数![]() 的导数
的导数![]() 的图象大致是( )
的图象大致是( )
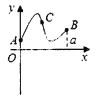
A. 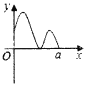 B.
B. 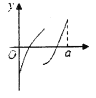 C.
C. 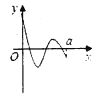 D.
D. 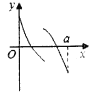
【答案】D
【解析】
当![]() 从
从![]() 运动到
运动到![]() 的过程中,面积先增加再减小,然后再增加再减小,由此求出结果。
的过程中,面积先增加再减小,然后再增加再减小,由此求出结果。
连接![]() ,
,![]() ,
,![]() ,以
,以![]() 为底,
为底,![]() 到
到![]() 的距离为高
的距离为高![]() .让
.让![]() 从
从![]() 运动到
运动到![]() ,明显
,明显![]() 是一个平滑的变化,这样
是一个平滑的变化,这样![]() 是平滑的变化.因为函数
是平滑的变化.因为函数![]() ,其中
,其中![]() 上为点
上为点![]() 到直线
到直线![]() 的距离
的距离![]() 为定值,当点
为定值,当点![]() 在
在![]() 时,
时,![]() 越来越大,
越来越大,![]() 也越来越大,即原函数递增,故导函数为正,当点
也越来越大,即原函数递增,故导函数为正,当点![]() 在
在![]() 时,
时,![]() 越来越小,
越来越小,![]() 也越来越小,即原函数递减,故导函数为负,变化率的绝对值由小变大,当点
也越来越小,即原函数递减,故导函数为负,变化率的绝对值由小变大,当点![]() 在
在![]() 时
时![]() 越来越大,
越来越大,![]() 也越来越大,即原函数递增,故导函数为正:变化率由大变小,当点
也越来越大,即原函数递增,故导函数为正:变化率由大变小,当点![]() 在
在![]() 时,
时,![]() 越来越小,
越来越小,![]() 也越来越小,即原函数递减,故导函数为负.故选D.
也越来越小,即原函数递减,故导函数为负.故选D.

【题目】目前共享单车基本覆盖饶城市区,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
(1)任选出一名学生,求他(她)骑行过共享单车的概率;
(2)随着单车投放数量增加,乱停乱放成为城市管理的问题,如表是本市某组织累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间关系图表:
之间关系图表:
累计投放单车数量 | 100000 | 120000 | 150000 | 200000 | 230000 |
乱停乱放单车数量 | 1400 | 1700 | 2300 | 3000 | 3600 |
计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() ,
,![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
(3)已知信州区、广丰区、上饶县、经开区四区中,其中有两个区的单车乱停乱放数量超过标准,在“大美上饶”活动中,检查组随机抽取两个区调查单车乱停乱放数量,![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
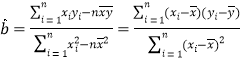 ,
,![]() ,
,
![]() ,
,![]()