题目内容
【题目】在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,
,![]() ,当角
,当角![]() 取最大值时,
取最大值时,![]() 的周长为
的周长为![]() ,则
,则![]() __________.
__________.
【答案】3
【解析】分析:根据题意由正弦定理得出cosA<0,A为钝角,cosAcosC≠0,由两角和的正弦函数公式,同角三角函数基本关系式可得出tanA=﹣3tanC,且tanC>0;由已知及基本不等式求出B取得最大值,可得C=B=![]() ,可求A,利用余弦定理可求a=
,可求A,利用余弦定理可求a=![]() b,结合已知求得b的值,进而可求a的值.
b,结合已知求得b的值,进而可求a的值.
详解:△ABC中,![]() sinB=cos(B+C)sinC,
sinB=cos(B+C)sinC,
∴![]() b=cos(B+C)c,即cosA=﹣
b=cos(B+C)c,即cosA=﹣![]() <0,∴A为钝角,
<0,∴A为钝角,
∴cosAcosC≠0;
由sinB=sin(A+C)=sinAcosC+cosAsinC=﹣2cosAsinC,
可得tanA=﹣3tanC,且tanC>0,
![]()
=![]()
当且仅当tanC=![]() 时取等号;
时取等号;
∴B取得最大值时,c=b=1,此时C=B=![]() .
.
∴A=![]() ,由a2=b2+c2﹣2bccosA,可得:a=
,由a2=b2+c2﹣2bccosA,可得:a=![]() b,
b,
∵三角形的周长为a+b+c=![]() b +b+b=2
b +b+b=2![]() .解得:b=
.解得:b=![]() ,可得:a=
,可得:a=![]() b =3.
b =3.
故答案为:3

【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
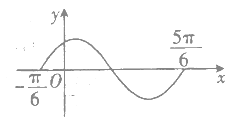
【题目】目前共享单车基本覆盖饶城市区,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
(1)任选出一名学生,求他(她)骑行过共享单车的概率;
(2)随着单车投放数量增加,乱停乱放成为城市管理的问题,如表是本市某组织累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间关系图表:
之间关系图表:
累计投放单车数量 | 100000 | 120000 | 150000 | 200000 | 230000 |
乱停乱放单车数量 | 1400 | 1700 | 2300 | 3000 | 3600 |
计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() ,
,![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
(3)已知信州区、广丰区、上饶县、经开区四区中,其中有两个区的单车乱停乱放数量超过标准,在“大美上饶”活动中,检查组随机抽取两个区调查单车乱停乱放数量,![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
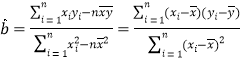 ,
,![]() ,
,
![]() ,
,![]()
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.

(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
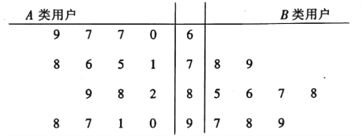
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
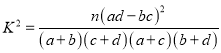 ,
, ![]() .
.