题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xoy中,已知直线![]() 的参数方程为
的参数方程为![]() 为参数,
为参数, ![]() 以原点O为极点,以
以原点O为极点,以![]() 轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)写出直线![]() 的极坐标方程和曲线C的直角坐标方程;
的极坐标方程和曲线C的直角坐标方程;
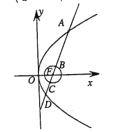
(2)若直线![]() 与曲线C相交于A,B 两点,求
与曲线C相交于A,B 两点,求![]() 的值.
的值.
【答案】(1)直线![]() 的极坐标方程为
的极坐标方程为![]() 和
和![]() 曲线的直角坐标方程为
曲线的直角坐标方程为![]() (2)
(2) ![]()
【解析】试题分析:(1)将直线![]() 的参数方程为
的参数方程为![]() 化为直角坐标方程,利用
化为直角坐标方程,利用![]() ,可得直线
,可得直线![]() 的极坐标方程,再利用简单的三角方程及极坐标的几何意义化简可得直线
的极坐标方程,再利用简单的三角方程及极坐标的几何意义化简可得直线![]() 的极坐标方程,由
的极坐标方程,由![]() 得
得![]() 利用
利用![]() 化简可得曲线C的直角坐标方程;(2)
化简可得曲线C的直角坐标方程;(2) ![]() 由
由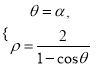 得,
得, ![]() 即
即![]() =
=![]() 同理可得
同理可得![]() =
=![]() ,从而可得
,从而可得![]() 的值.
的值.
试题解析:(1)由参数方程![]() 得当
得当![]() 时,直线
时,直线![]() 为
为![]() 其极坐标方程为
其极坐标方程为![]() 和
和![]()
当![]() 时,消去参数
时,消去参数![]() 得
得![]() .因为
.因为![]() ,所以直线
,所以直线![]() 的极坐标方程为
的极坐标方程为![]() 和
和![]()
综合以上, 直线![]() 的极坐标方程为
的极坐标方程为![]() 和
和![]()
由![]() 得
得![]() 因为
因为![]() 所以
所以![]() 化简得曲线的直角坐标方程为
化简得曲线的直角坐标方程为![]()
(2)设![]() 由
由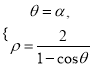 得,
得, ![]() 即|OA|=
即|OA|=![]() 同理
同理
由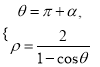 得,
得, ![]() 即|OB|=
即|OB|=![]() 所以
所以![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.