Question

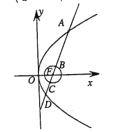
【题目】如图，已知抛物线的焦点为，直线过点且依次交抛物线及圆于四点，则的最小值为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】∵y2=x，焦点F（，0），准线 l0：x=﹣，由圆：（x﹣）2+y2=2圆心（，0），半径为；

由抛物线的定义得：|AF|=xA+，

又∵|AF|=|AB|+，∴|AB|=xA+同理：|CD|=xD+，

当AB⊥x轴时，则xD=xA=，∴|AB|+4|CD|=15．

当AB的斜率存在且不为0，设AB：y=k（x﹣）时，代入抛物线方程，得：

k2x2﹣（k2+）x+8k2=0，

∴xAxD=8，xA+xD=，

∴|AB|+4|CD|=（xA+）+4（xD+）=5+xA+4xD≥+2=13．

当且仅当xA=4xD，即xA=2，xD=时取等号，

综上所述|AB|+4|CD|的最小值为

故答案为：C。