题目内容
【题目】已知椭圆![]() +
+![]() =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,![]() )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据![]() 与离心率可求得a,b,c的值,从而就得到椭圆的方程;(2)设出直线的方程
与离心率可求得a,b,c的值,从而就得到椭圆的方程;(2)设出直线的方程![]() ,并与椭圆方程联立消去y可得到关于x的一元二次方程,然后利用中点坐标公式与分类讨论的思想进行解决.
,并与椭圆方程联立消去y可得到关于x的一元二次方程,然后利用中点坐标公式与分类讨论的思想进行解决.
试题解析:(1)![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
椭圆的标准方程为![]() .
.
(2)已知![]() ,设直线的方程为
,设直线的方程为![]() ,
,![]() -,
-,
联立直线与椭圆的方程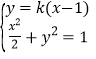 ,化简得:
,化简得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 的中点坐标为
的中点坐标为![]() .
.
①当![]() 时,
时,![]() 的中垂线方程为
的中垂线方程为![]() ,
,
∵![]() ,∴点
,∴点![]() 在
在![]() 的中垂线上,将点
的中垂线上,将点![]() 的坐标代入直线方程得:
的坐标代入直线方程得:
![]() ,即
,即![]() ,
,
解得![]() 或
或![]() .
.
②当![]() 时,
时,![]() 的中垂线方程为
的中垂线方程为![]() ,满足题意,
,满足题意,
∴斜率![]() 的取值为
的取值为![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目