题目内容
20.(文)在△ABC中,已知sinA=$\frac{5}{13}$,cosB=$\frac{3}{5}$,则cosC=-$\frac{16}{65}$;(理)在△ABC中,已知tanA,tanB是x的方程x2+p(x+1)+1=0的两个根,则∠C=$\frac{3π}{4}$.
分析 (文)由条件利用同角三角函数的基本关系,求出sinB、cosA的值,再根据cosC=-cos(A+B)=-cosAcosB+sinAsinB 计算求得结果.
(理)利用韦达定理、两角和的正切公式求得 tan(A+B)的值,可得A+B的值,进而求得C的值.
解答 解:(文)△ABC中,∵已知sinA=$\frac{5}{13}$∈(0,$\frac{1}{2}$),cosB=$\frac{3}{5}$∈($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),
∴B∈($\frac{π}{4}$,$\frac{π}{3}$),A∈(0,$\frac{1}{2}$ ),或A∈($\frac{5π}{6}$,π)(舍去,不满足三角形内角和公式),
∴sinB=$\sqrt{{1-cos}^{2}B}$=$\frac{4}{5}$,cosA=$\sqrt{{1-sin}^{2}A}$=$\frac{12}{13}$,
则cosC=-cos(A+B)=-cosAcosB+sinAsinB=-$\frac{12}{13}×\frac{3}{5}$+$\frac{5}{13}×\frac{4}{5}$=-$\frac{16}{65}$,
故答案为:$-\frac{16}{65}$.
(理)在△ABC中,已知tanA,tanB是x的方程x2+p(x+1)+1=0的两个根,
故有tanA+tanB=-p,tanA•tanB=p+1,∴tan(A+B)=$\frac{tanA+tanB}{1-tanAtanB}$=$\frac{-p}{-p}$=1,
在结合A+B∈(0,π),可得A+B=$\frac{π}{4}$,∴C=π-(A+B)=$\frac{3π}{4}$,
故答案为:$\frac{3π}{4}$.
点评 本题主要考查同角三角函数的基本关系,诱导公式,韦达定理以及两角和差的三角公式,属于基础题.

 53随堂测系列答案
53随堂测系列答案| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
| A. | R | B. | [0,+∞) | C. | (-∞,0] | D. | [-1,1] |
| A. | 减函数且最小值是2 | B. | .减函数且最大值是2 | ||
| C. | 增函数且最小值是2 | D. | 增函数且最大值是2 |
| A. | 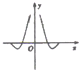 | B. | 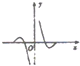 | C. | 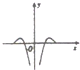 | D. | 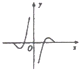 |