题目内容
4.已知a,b,c分别为△ABC的三个内角A,B,C的对边,且a2+b2=c2+ab,4sinAsinB=3,则tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$=$\sqrt{3}$.分析 运用余弦定理,可得C=60°,设A=60°-α,C=60°+α,代入化简整理可得A=B=60°,即可得到所求.
解答 解:a2+b2=c2+ab,
即为a2+b2-c2=ab,
cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
由C为三角形的内角,则C=60°,
设A=60°-α,B=60°+α,
则4sinAsinB=3,即为sin(60°-α)sin(60°+α)=$\frac{3}{4}$,
即有($\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα)($\frac{\sqrt{3}}{2}$cosα+$\frac{1}{2}$sinα)=$\frac{3}{4}$,
即$\frac{3}{4}$cos2α-$\frac{1}{4}$sin2α=$\frac{3}{4}$,即$\frac{3}{4}$-sin2α=$\frac{3}{4}$,
解得sinα=0,(-60°<α<60°),
即有α=0°,
则A=B=60°,
则tan$\frac{A}{2}$+tan$\frac{B}{2}$+tan$\frac{C}{2}$=3tan30°=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查余弦定理的运用,三角函数的化简和求值,考查运算能力,属于中档题.

练习册系列答案
相关题目
13.有一个圆心为(a,b),半径为c的定圆如图所示,则直线ax-by+c=0与直线x+y-1=0的交点在( )
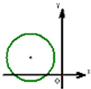

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |