题目内容
16.已知两点A(-4,3),B(3,2),过点P(0,-1)的直线l与线段AB有公共点.(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角的取值范围.
分析 (1)如图所示,由于过点P(0,-1)的直线l与线段AB有公共点.可得kl≥kPB,或kl≤kPA.即可直线l的斜率k的取值范围.
(2)由$tan\frac{π}{4}$=1,$tan\frac{3π}{4}$=-1,即可得出直线l的倾斜角的取值范围.
解答 解:(1)如图所示,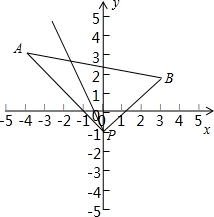
∵kPA=$\frac{3-(-1)}{-4-0}$=-1,kPB=$\frac{2-(-1)}{3-0}$=1,
又过点P(0,-1)的直线l与线段AB有公共点.
∴kl≥1,或kl≤-1.
∴直线l的斜率k的取值范围是(-∞,-1]∪[1,+∞).
(2)由$tan\frac{π}{4}$=1,$tan\frac{3π}{4}$=-1,利用(1)可得:
直线l的倾斜角的取值范围是$[\frac{π}{4},\frac{3π}{4}]$.
点评 本题考查了直线的向量计算公式及其应用,考查了数形结合思想方法与计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
6.在数列{an}中,a1=2,an+1=an+ln(1+$\frac{1}{n}$),则a5=( )
| A. | 1+ln2 | B. | 2+ln3 | C. | 3+ln5 | D. | 2+ln5 |