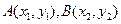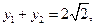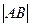题目内容
过圆锥曲线焦点的直线与此圆锥曲线交于P1、P2两点,以P1P2为直径的圆与此焦点对应的准线相切,则此圆锥曲线是( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.不确定 |
C
如图所示,设过抛物线y2=2px(p>0)焦点F的弦为AB,弦中点为M,A、B、M在准线x=-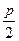 上的垂足为A′、B′、M′,则MM′为梯形AA′B′B的中位线.
上的垂足为A′、B′、M′,则MM′为梯形AA′B′B的中位线.
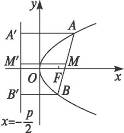
所以有|MM′|=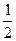 (|AA′|+|BB′|).
(|AA′|+|BB′|).
由抛物线定义|AA′|+|BB′|=|AF|+|BF|=|AB|,
∴|MM′|=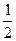 |AB|.
|AB|.
∴以过焦点F的直线与抛物线的交点所成线段AB为直径的圆与准线相切.
故选C.
同理可得当相离时,是双曲线;当相交时,是椭圆.以上可作为结论记住,提高解题速度.
 上的垂足为A′、B′、M′,则MM′为梯形AA′B′B的中位线.
上的垂足为A′、B′、M′,则MM′为梯形AA′B′B的中位线.
所以有|MM′|=
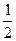 (|AA′|+|BB′|).
(|AA′|+|BB′|).由抛物线定义|AA′|+|BB′|=|AF|+|BF|=|AB|,
∴|MM′|=
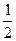 |AB|.
|AB|.∴以过焦点F的直线与抛物线的交点所成线段AB为直径的圆与准线相切.
故选C.
同理可得当相离时,是双曲线;当相交时,是椭圆.以上可作为结论记住,提高解题速度.

练习册系列答案
相关题目
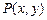 到点
到点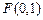 与到直线
与到直线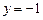 的距离相等,求点
的距离相等,求点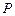 的轨迹
的轨迹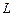 的方程;
的方程;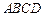 的三个顶点
的三个顶点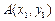 ,
,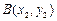 ,
,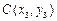 (
(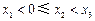 )在(1)中的曲线
)在(1)中的曲线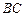 的斜率为
的斜率为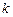 ,
,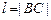 ,求
,求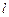 关于
关于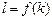 ;
;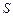 的最小值.
的最小值.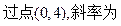 -1的直线与抛物线
-1的直线与抛物线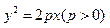 交于两点A,B,如果
交于两点A,B,如果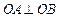 (O为原点)求P的值及抛物线的焦点坐标。
(O为原点)求P的值及抛物线的焦点坐标。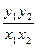 的值为________________.
的值为________________.