题目内容
抛物线y=ax2(a>0)与直线y=kx+b(k≠0)有两个公共点,其横坐标分别是x1、x2.而直线y=kx+b与x轴交点的横坐标是x3,则x1、x2、x3之间的关系是( )
| A.x3=x1+x2 |
B.x3=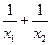 |
| C.x1x3=x1x2+x2x3 |
| D.x1x2=x1x3+x2x3 |
D
方法一:(特值法)
取a=1,k=1,b=0,
则x1=0,x2=1,x3="0," 可排除A、B.
再取a=1,k=1,b=1,可得x1+x2=1,x1x2=-1,x3=-1.检验C、D可知D选项适合.
方法二:(直接法)
把y=kx+b代入y=ax2,得ax2-kx-b=0,x1+x2=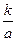 ,x1x2=-
,x1x2=-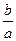 .
.
又x3=-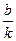 ,
,
∴x1x2=(x1+x2)x3.
取a=1,k=1,b=0,
则x1=0,x2=1,x3="0," 可排除A、B.
再取a=1,k=1,b=1,可得x1+x2=1,x1x2=-1,x3=-1.检验C、D可知D选项适合.
方法二:(直接法)
把y=kx+b代入y=ax2,得ax2-kx-b=0,x1+x2=
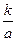 ,x1x2=-
,x1x2=-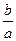 .
.又x3=-
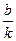 ,
,∴x1x2=(x1+x2)x3.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
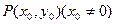 的切线方程为
的切线方程为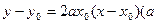 为常数).
为常数).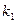 的直线PA与抛物线的另一交点为A,斜率为
的直线PA与抛物线的另一交点为A,斜率为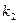 的直线PB与抛物线的另一交点为B(A、B两点不同),且满足
的直线PB与抛物线的另一交点为B(A、B两点不同),且满足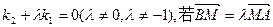 ,求证线段PM的中点在y轴上;
,求证线段PM的中点在y轴上;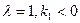 时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围. 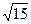 ,求抛物线方程.
,求抛物线方程.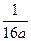 )
)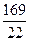 x
x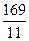 x
x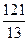 y
y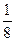
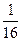
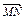 =2
=2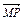 ,
,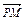 ⊥
⊥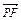 ,当点P
,当点P